【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】B
【解析】
试题解析:①∵抛物线的对称轴为直线x=-![]() =2,
=2,
∴b=-4a,即4a+b=0,故本结论正确;
②∵当x=-3时,y<0,
∴9a-3b+c<0,
即9a+c<3b,故本结论错误;
③∵抛物线与x轴的一个交点为(-1,0),
∴a-b+c=0,
而b=-4a,
∴a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a -10a =-30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,故本结论正确;
④∵对称轴为直线x=2,
∴当-1<x<2时,y的值随x值的增大而增大,
当x>2时,y随x的增大而减小,故本结论错误;
⑤∵抛物线的对称轴为直线x=2,与x轴的一个交点为(-1,0),
∴抛物线与x轴的另外一个交点为(5,0),
∴当函数值y<0时,自变量x的取值范围是x<-1或x>5,故本结论正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a-b=8,a2+b2=82,则ab的值为( )
A. 9 B. -9 C. 27 D. -27
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.
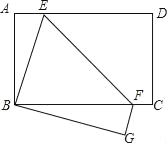
-
科目: 来源: 题型:
查看答案和解析>>【题目】半径分别为3cm和4cm的两圆内切,这两圆的圆心距为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与直线y=2x+3交于点M(0,3), A(a,15).点B是抛物线上M,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线MA交于点C,E.以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),请写出m,n之间的关系式________________ .
与直线y=2x+3交于点M(0,3), A(a,15).点B是抛物线上M,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线MA交于点C,E.以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),请写出m,n之间的关系式________________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
相关试题

