【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上的点,
上的点,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 边上的点,连接
边上的点,连接![]() ,若线段
,若线段![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
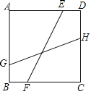
过点B作BK∥EF交AD于K,作BM∥GH交CD于M,可得∠KBM=45°,作∠MBN=45°交DC的延长线于N,求出∠ABK=∠CBN,然后利用“角边角”证明△ABK和△CBN全等,根据全等三角形对应边相等可得BN=BK,AK=CN,利用勾股定理列式求出AK,过点M作MP⊥BN于P,可得△BMP是等腰直角三角形,设GH=BM=x,表示出MP,然后利用∠N的正切值列出方程求解即可.
如图,过点B作BK∥EF交AD于K,作BM∥GH交CD于M,
则BK=EF=![]() ,BM=GH,
,BM=GH,
∵线段GH与EF的夹角为45°,
∴∠KBM=45°,
∴∠ABK+∠CBM=90°-45°=45°,
作∠MBN=45°交DC的延长线于N,
则∠CBN+∠CBM=45°,
∴∠ABK=∠CBN,
在△ABK和△CBN中,
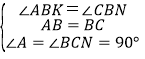 ,
,
∴△ABK≌△CBN(ASA),
∴BN=BK,AK=CN,
在Rt△ABK中,AK=![]() =1,
=1,
过点M作MP⊥BN于P,
∵∠MBN=45°,
∴△BMP是等腰直角三角形,
设GH=BM=x,则BP=MP=![]() BM=
BM=![]() x,
x,
∵tan∠N=![]() ,
,
∴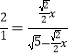 ,
,
解得x=![]() ,
,
所以GH=![]() ,
,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是

A.①②③④B.①②③C.②④D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:

(1)将△ABC向下平移5单位长度,画出平移后的
 并写出点A对应点
并写出点A对应点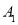 的坐标;
的坐标;(2)画出
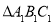 关于y轴对称的
关于y轴对称的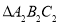 并写出
并写出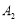 的坐标;
的坐标;(3)
 =______.(直接写答案)
=______.(直接写答案)(4)在x轴上求作一点P,使PA+PB最小(不写作法,保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
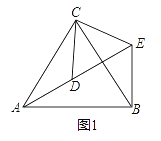
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
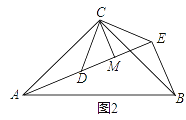
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
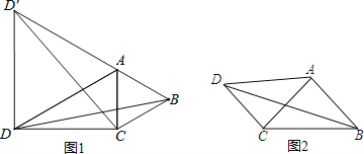
查看答案和解析>>【题目】如图,在△ACD中,AD=9,CD=3
 ,△ABC中,AB=AC.
,△ABC中,AB=AC.(1)如图1,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
①求证:BD=CD′;
②求BD的长.
(2)如图2,若∠CAB=90°,∠ADC=45°,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA=OB,△OAB的面积是2.
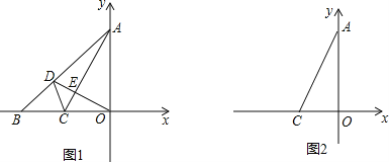
(1)求线段OB的中点C的坐标.
(2)连结AC,过点O作OE⊥AC于E,交AB于点D.
①直接写出点E的坐标.
②连结CD,求证:∠ECO=∠DCB;
(3)点P为x轴上一动点,点Q为平面内一点,以点A.C.P.Q为顶点作菱形,直接写出点Q的坐标.
相关试题

