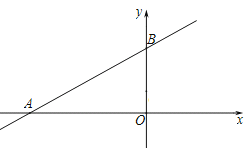
【题目】如图,一次函数图象![]() 与
与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() .
.
(1)判断点![]() 是否在该函数的图象上?
是否在该函数的图象上?
(2)求点![]() 的坐标;
的坐标;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的面积为
的面积为![]() ?若存在,求出所有满足
?若存在,求出所有满足![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() 不在该函数图象上;(2)B(0,2),A(-3,0);(3)(1,
不在该函数图象上;(2)B(0,2),A(-3,0);(3)(1,![]() )或(-1,
)或(-1,![]() )
)
【解析】
(1)将x=-6代入直线AB的解析式,然后根据纵坐标判断即可;
(2)令y=0和x=0即可求出点A,B的坐标;
(3)先设点D的坐标为(a,![]() ),从而可得三角形BOD以OB为底边,a的绝对值为高,进而表示出三角形BOD面积,然后根据已知面积求出a的值,即可确定D的坐标.
),从而可得三角形BOD以OB为底边,a的绝对值为高,进而表示出三角形BOD面积,然后根据已知面积求出a的值,即可确定D的坐标.
(1)当x=-6时,![]() ,
,
∴![]() 不在该函数图象上;
不在该函数图象上;
(2)令x=0,则![]() =2,
=2,
∴B(0,2),
令y=0,则0=![]() ,
,
∴x=-3,
∴A(-3,0);
(3)设D坐标为(a,![]() ),
),
∵B(0,2),
∴OB=2
根据题意得:S△BOD=![]() OB·|a|=
OB·|a|=![]() ×2·|a|=|a|,
×2·|a|=|a|,
∵S△BOD=1,
∴|a|=1,
解得:a=1或a=-1,
∴D坐标为(1,![]() )或(-1,
)或(-1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲开车从距离
 市
市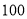 千米的
千米的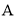 市出发去
市出发去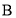 市,乙从同一路线上的
市,乙从同一路线上的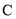 市出发也去往
市出发也去往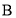 市,二人离
市,二人离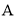 市的距离与行驶时间的函数关系如图所示(
市的距离与行驶时间的函数关系如图所示(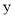 代表距离,
代表距离,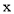 代表时间).
代表时间).(1)
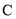 市离
市离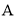 市的距离是 千米;
市的距离是 千米;(2)甲的速度是 千米/时,乙的速度是 千米/时;
(3)甲比乙早几小时到达
 市?
市?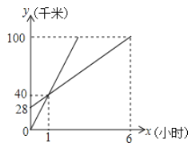
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某位老师在讲“实数”时,画了一个图,即“以数轴的单位长线段为边作一个正方形,然后以原点为圆心,正方形的对角线长为半径画弧交数轴于一点
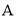 ”,作这样的图用来说明:
”,作这样的图用来说明: 
作图:请你在数轴上找出
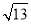 对应的点.
对应的点. -
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军和小刚两位同学在学习”概率“时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次试验,实验的结果如下:
向上点数
1
2
3
4
5
6
出现次数
7
9
6
8
20
10
(1)计算“2点朝上”的频率和“5点朝上”的频率.
(2)小军说:“根据实验,一次实验中出现3点朝上的概率是
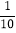 ”;小军的这一说法正确吗?为什么?
”;小军的这一说法正确吗?为什么?(3)小刚说:“如果掷600次,那么出现6点朝上的次数正好是100次.”小刚的这一说法正确吗?为什么?
相关试题

