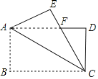
【题目】如图,矩形纸片![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的长等于( )
的长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
由折叠的性质得到AE=AB,∠E=∠B=90°,易证Rt△AEF≌Rt△CDF,即可得到结论EF=DF;易得FC=FA,设FA=x,则FC=x,FD=6-x,在Rt△CDF中利用勾股定理得到关于x的方程x2=42+(6-x)2,解方程求出x即可.
∵矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,
∴AE=AB,∠E=∠B=90°,
又∵四边形ABCD为矩形,
∴AB=CD,
∴AE=DC,
而∠AFE=∠DFC,
∵在△AEF与△CDF中,
 ,
,
∴△AEF≌△CDF(AAS),
∴EF=DF;
∵四边形ABCD为矩形,
∴AD=BC=6,CD=AB=4,
∵Rt△AEF≌Rt△CDF,
∴FC=FA,
设FA=x,则FC=x,FD=6-x,
在Rt△CDF中,CF2=CD2+DF2,即x2=42+(6-x)2,解得x=![]() ,
,
则FD=6-x=![]() .
.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )

A. 3 B. 2 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )

A. 5对 B. 6对 C. 7对 D. 8对
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在
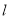 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?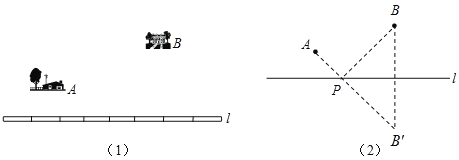
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
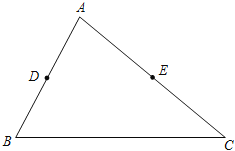
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3
 B. 28-3
B. 28-3 C. 28-4
C. 28-4 D. 29-5
D. 29-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为
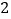 的正方形的中心
的正方形的中心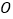 为端点,引两条相互垂直的射线,分别与正方形的边交于
为端点,引两条相互垂直的射线,分别与正方形的边交于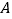 、
、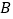 两点,则线段
两点,则线段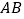 的取值范围是________.
的取值范围是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为
 .
.(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
相关试题

