【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
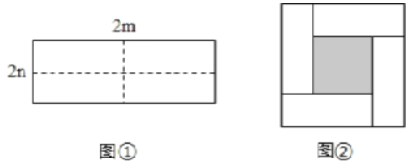
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
参考答案:
【答案】(1)(m+n)![]() 4mn,(mn)
4mn,(mn)![]() ;(2)(m+n)
;(2)(m+n)![]() 4mn=(mn)
4mn=(mn)![]() ;(3)±5.
;(3)±5.
【解析】
(1)观察图形可确定:方法一,大正方形的面积为(m+n)![]() ,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)
,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)![]() -4mn;
-4mn;
方法二,图2中阴影部分为正方形,其边长为m-n,所以其面积为(m-n)![]() .
.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)![]() -4mn=(m-n)
-4mn=(m-n)![]() .
.
(3)根据(2)的关系式代入计算即可求解.
(1)方法一:S小正方形=(m+n) ![]() 4mn.
4mn.
方法二:S小正方形=(mn) ![]() .
.
(2)(m+n)![]() ,(mn)
,(mn)![]() ,mn这三个代数式之间的等量关系为(m+n)
,mn这三个代数式之间的等量关系为(m+n)![]() 4mn=(mn)
4mn=(mn)![]() .
.
(3)∵x+y=9,xy=14,
∴xy=![]() =±5.
=±5.
故答案为:(m+n)![]() 4mn,(mn)
4mn,(mn) ![]() ;(m+n)
;(m+n)![]() 4mn=(mn)
4mn=(mn)![]() ,±5.
,±5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 内角
内角 的平分线,
的平分线, 是
是 外角
外角 的平分线,
的平分线, 是
是 外角
外角 的平分线,以下结论不正确的是( )
的平分线,以下结论不正确的是( )
A.
 B.
B.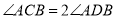
C.
 D.
D. 平分
平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有 人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是 度;
(4)已知该校共有学生2500人,根据调查结果估计该校喜欢体操的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___),
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司经销甲种型号电脑,受疫情影响,电脑价格不断下降,今年四月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的甲种电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年四月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再进销售价为6000元的乙种型号电脑,四月份甲、乙两种电脑共销售15台,如果销售额不低于8万元,则乙种型号电脑销售不低于多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,将纸片折叠,使顶点B落在边AD上的点为E,折痕的一端G点在BC上(BG<GC),另一端F落在矩形的边上,BG=5.
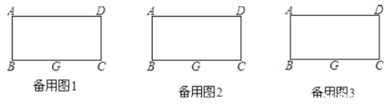
(1)请你在备用图中画出满足条件的图形;
(2)求出AF的长.
相关试题

