【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)
(1)求出两个动点运动的速度;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;
(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.
![]()
参考答案:
【答案】(1)A:1;B:4;(2)t=![]() ;(3) t=
;(3) t=![]() 秒,B追上A, C 点运动64个单位
秒,B追上A, C 点运动64个单位
【解析】试题分析:(1)设A点运动速度为x单位长度/秒,则B点运动速度为4x单位长度/秒.
由题意得:3x+3×4x=15,解得:x=1所以A点的运动速度是1单位长度/秒,B点的速度是4单位长度/秒;
在数轴上表示出其位置即可.
(2)设y秒后,原点恰好处在A、B的正中间.由题意得:y+3=12-4y解得:y=![]() ,所以,经过
,所以,经过![]() 秒后,原点恰处在A、B的正中间;(3)设B追上A需时间z秒,则:4×z-1×z=2×(
秒后,原点恰处在A、B的正中间;(3)设B追上A需时间z秒,则:4×z-1×z=2×(![]() +3)解得:z=
+3)解得:z=![]() ,
,
20×![]() =64.所以C点行驶的路程是64长度单位.
=64.所以C点行驶的路程是64长度单位.
试题解析:(1)设A点运动速度为x单位长度/秒,则B点运动速度为4x单位长度/秒.
由题意得:3x+3×4x=15
解得:x=1
∴A点的运动速度是1单位长度/秒,B点的速度是4单位长度/秒;
![]()
(2)设y秒后,原点恰好处在A、B的正中间.
由题意得:y+3=12-4y,解得:y=![]()
∴经过![]() 秒后,原点恰处在A、B的正中间;
秒后,原点恰处在A、B的正中间;
(3)设B追上A需时间z秒,则:
4×z-1×z=2×(![]() +3) 解得:z=
+3) 解得:z=![]() ,
,
20×![]() =64.
=64.
∴C点行驶的路程是64长度单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
A.长方形
B.平行四边形
C.正五边形
D.等边三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列命题的真假,并给出证明
(1)两个锐角的和是钝角;
(2)若a>b,则a2>b2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
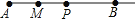
-
科目: 来源: 题型:
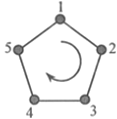
查看答案和解析>>【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”. 如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,那么第二次“移位”后他所处的顶点的编号为____________。第181次“移位”后,则他所处顶点的编号是___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能很快算出19952吗?请按以下步骤表达探索过程(填空):
通过计算,探索规律:
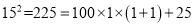 ,
, 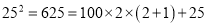 ,
, ,
, 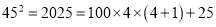
(1)
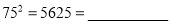 ,
,(2)从第(1)题的结果,归纳、猜想得
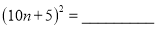
(3)请根据上面的归纳猜想,算出

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A.任意三角形的内角和都是180°
B.三角形按边分可分为不等边三角形和等腰三角形
C.三角形的中线、角平分线、高都是线段
D.三角形的一个外角大于任何一个内角
相关试题

