【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)若DE=CE,求证:AB∥DE;
(2)若DC=2,求证:△ABD≌△DCE;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由;

参考答案:
【答案】(1)见解析;(2)见解析;(3) 可以, 115°或100°,理由见解析
【解析】
(1)根据等边对等角可得∠B=∠C,∠C=∠EDC,所以∠B=∠EDC,根据平行线的判定可得AB∥DE;
(2)利用∠DEC+∠EDC=130°,∠ADB+∠EDC=130°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
(3)分两种情况进行讨论,根据三角形的外角性质,可得当∠BDA的度数为115°或100°时,△ADE的形状是等腰三角形.
(1)证明:∵DE=CE,∠C=50°,
∴∠C=∠EDC=50°.
∵∠B=∠C=50°,
∴∠B=∠EDC,
∴AB∥DE;
(2)证明:∵AB=AC=2,DC=2,
∴AB=DC,
∵∠B=∠C=50°,∠ADE=50°,
∴∠BDA+∠CDE=130°,
∠CED+∠CDE=130°,
∴∠BDA=∠CED,
∴△ABD≌△DCE(AAS)
(3)解:可以.有以下三种可能:
①由(1)得:△ABD≌△DCE,得AD=DE,
则有∠DAE=∠DEA=65°.
∴∠BDA=∠CED=65°+50°=115°;
②由(2)得∠BDA=∠CED.
∵点D在线段BC上运动(点D不与B、C重合),
∴AD≠AE;
③当EA=ED时,∠EAD=∠ADE=50°,
∴∠BDA=∠CED=50°+50°=100°.
故答案为:(1)见解析;(2)见解析;(3) 可以, 115°或100°,理由见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( ).

A.3
B.
C.5
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)求证:AC=CB; (2)若AC=12 cm,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角尺按如图所示叠放在一起,其中点
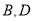 重合,若固定三角形
重合,若固定三角形 ,将三角形
,将三角形 绕点
绕点 顺时针旋转一周,共有 _________次 出现三角形
顺时针旋转一周,共有 _________次 出现三角形 的一边与三角形AOB的某一边平行.
的一边与三角形AOB的某一边平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
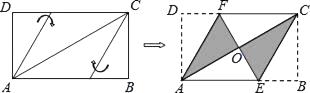
A.1
B.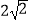
C.
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:

(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
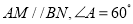 ,点
,点 是射线
是射线 上一动点(与点
上一动点(与点 不重合),
不重合), 分别平分
分别平分 和
和 ,分别交射线
,分别交射线 于点
于点

 若点
若点 运动到某处时,恰有
运动到某处时,恰有 ,此时
,此时 与
与 有何位置关系?请说明理由.
有何位置关系?请说明理由. 在点
在点 运动的过程中,
运动的过程中, 与
与 之间的关系是否发生变化?若不变,请写出它们的关系并说明理由;若变化,请写出变化规律.
之间的关系是否发生变化?若不变,请写出它们的关系并说明理由;若变化,请写出变化规律.
相关试题

