【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+![]() =0.
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
参考答案:
【答案】(1)y=﹣2x+4;(2)m=1.
【解析】
(1)根据非负数的性质可求得p、q,可求得A、B坐标,利用待定系数法可求得直线AB的解析式;
(2)根据A、B坐标,可求出AB及AB中点的C坐标,设M坐标为(x,mx),则MC=![]() AB,且M点在线段AB的垂直平分线上,可求得垂直平分线的方程,则可求得M的值.
AB,且M点在线段AB的垂直平分线上,可求得垂直平分线的方程,则可求得M的值.
解:(1)根据题意可得:p﹣2=0,解得 p=2,
根据题意可得:q﹣4=0 解得:q=4,
设直线AB的解析式为y=kx+4( k≠0)
将A(2,0)代入得
2k+4=0
k=﹣2
∴AB的解析式为y=﹣2x+4;
(2)过M点作MH⊥y轴于H,过M点作MN⊥x轴于N
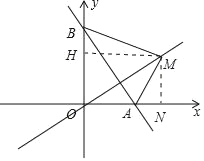
∴∠BHM=∠MNA=90°
∵∠BON=90°
∴∠HMN=90°
∴∠HMA+∠AMN=90°
∵△ABM是以AB为底的等腰直角三角形
∴MB=MA,∠BMA=90°
∴∠HMA+∠BMH=90°
∴∠AMN=∠BMH
∴△BHM≌△AMN
∴MH=MN,
设M的坐标为(x,y)
则x=y
∴mx=x
∴m=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
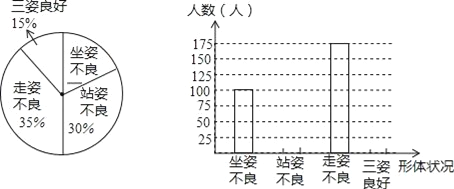
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.


某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调
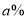 (降价后售价不低于进价),雄蟹的价格上涨
(降价后售价不低于进价),雄蟹的价格上涨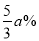 ,同时雌蟹的销量较九月下降了
,同时雌蟹的销量较九月下降了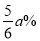 ,雄蟹的销量上升了
,雄蟹的销量上升了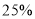 ,结果十月份的销售额比九月份增加了1000元,求a的值.
,结果十月份的销售额比九月份增加了1000元,求a的值. -
科目: 来源: 题型:
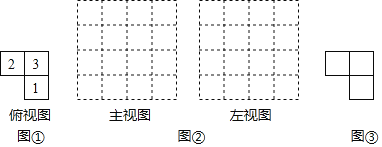
查看答案和解析>>【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如图①,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸图②中分别画出这个几何体的主视图和左视图.
(2)根据三视图,这个组合几何体的表面积为多少个平方单位?(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,如图③,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大(包括底面积)仿照图①,将数字填写在图③的正方形中.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的证明过程,指出其错误.(在错误部分下方划线)已知△ABC,求证:∠A+∠B+∠C=180°
(1)证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(作图)
∴∠2=∠B(内错角相等两直线平行)
∵∠1=∠C(作图)
∴∠B+∠C+∠3=∠2+∠1+∠3(等量代换)
∠2+∠l+∠3=180°(周角的定义)
即∠BAC+∠B+∠C=180°(等量代换)
(2)类比探究:请同学们参考图2,模仿(1)的解决过程,避免(1)中的错误,试说明求证:∠A+∠B+∠C=180°
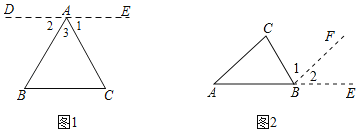
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费
 自来水销售费用
自来水销售费用 污水处理费用)
污水处理费用)自来水销售价格
污水处理价格
每户每月用水量
单价:元
 吨
吨单价:元
 吨
吨17吨及以下
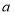
0.80
超过17吨不超过30吨的部分

0.80
超过30吨的部分
6.00
0.80
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求
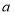 ,
, 的值.
的值.(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
-
科目: 来源: 题型:
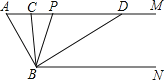
查看答案和解析>>【题目】综合与探究:如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合).BC,BD别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠ABN、∠CBD的度数;根据下列求解过程填空.
解:∵AM∥BN,
∴∠ABN+∠A=180°
∵∠A=60°,
∴∠ABN= ,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP、∠PBN= ,( )
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP= .
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
相关试题

