【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

参考答案:
【答案】(1)1;30 (2)图像见详解;3 (3) ![]() h.
h.
【解析】
(1)根据函数图象得到小张在路上停留的时间,由图象中的数据可以得到小张从乙地返回时骑车的速度;
(2)根据小王对应的函数解析式可以得到相应的函数图象,根据函数图象可以得到小王与小张在途中的次数;
(3)根据图象可以得到当4≤x≤6时,小张对应的函数解析式,然后与小王对应的函数解析式联立,即可解答本题.
解:(1)由图象可知,小张在路上停留1小时,他从乙地返回时骑车的速度为:60![]() (6-4)=30千米/时,
(6-4)=30千米/时,
故答案为:1,30;
(2)如右图所示, 
图中实线表示y=10x+10,由图象可知,小王与小张在途中相遇3次,
故答案为:3;
(3)设当4≤x≤6时,小张对应的函数解析式为y=kx+b,得:
![]() ,解得:k=-30,b=180,
,解得:k=-30,b=180,
![]() 当4≤x≤6时,小张对应的函数解析式为y=-30x+180,
当4≤x≤6时,小张对应的函数解析式为y=-30x+180,
![]() 当4≤x≤6时,小王对应的函数解析式为y=10x+10,
当4≤x≤6时,小王对应的函数解析式为y=10x+10,
![]()
![]() ,解得:
,解得: ,
,
即小王与小张在途中第三次相遇的时间为![]() h
h
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示,设点A,B,C所对应的数的和是
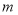 .
.
(1)若以点B为原点,则点C所对应的数是 ,若以点C的原点,则
 的值是 .
的值是 .(2)若原点O在图中数轴上,且点C到原点的距离为4,求
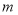 的值.
的值.(3)动点P从点A出发,以每秒2个单位长度的速度向终点C移动,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,
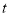 秒后,P,Q两点间距离为2?(请直接写出答案)
秒后,P,Q两点间距离为2?(请直接写出答案)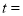 .
. -
科目: 来源: 题型:
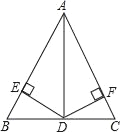
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
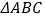 中,点
中,点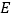 在
在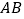 上,点
上,点 在
在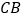 的延长线上,且
的延长线上,且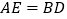 .试探索以下问题:
.试探索以下问题: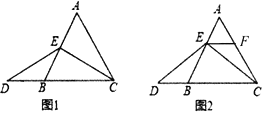
(1)当点
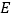 为
为 的中点时,如图1,求证:
的中点时,如图1,求证: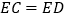 .
.(2)如图2,当点
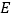 不是
不是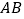 的中点时,过点
的中点时,过点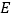 作
作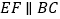 ,交
,交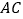 于点
于点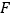 ,求证:
,求证: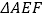 是等边三角形.
是等边三角形.(3)在(2)的条件下,
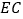 与
与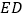 还相等吗?请说明理由.
还相等吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
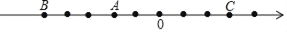
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的
 ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
相关试题

