【题目】在一条不完整的数上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示,设点A,B,C所对应的数的和是![]() .
.
![]()
(1)若以点B为原点,则点C所对应的数是 ,若以点C的原点,则![]() 的值是 .
的值是 .
(2)若原点O在图中数轴上,且点C到原点的距离为4,求![]() 的值.
的值.
(3)动点P从点A出发,以每秒2个单位长度的速度向终点C移动,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,![]() 秒后,P,Q两点间距离为2?(请直接写出答案)
秒后,P,Q两点间距离为2?(请直接写出答案)![]() .
.
参考答案:
【答案】(1)7,-17;(2)![]() ;
;![]() ;(3)t=1或5.
;(3)t=1或5.
【解析】
(1)根据已知点A到点B的距离为3和点C到点B的距离为7求出即可;
(2)分为两种情况,当O在C的左边时,当O在C的右边时,求出每种情况A、B、C对应的数,即可求出m;
(3)分为两种情况,当P在Q的左边时,当P在Q的左边时,假如C为原点,求出P、Q对应的数,列出算式,即可求出t.
(1)(1)当B为原点时,点C对应的数是7;当以C为原点时,A、B对应的数分别为-7,-10,m=-10+(-7)+0=-17,
故答案为:7,-17;
(2)若点C在原点的左边,则![]() ,
,![]() ,
,![]()
![]()
若点C在原点的右边,则![]() ,
,![]() ,
,![]()
![]()
(3)假如以C为原点,则A、B、C对应的数为-10,-7,0,Q对应的数是-(7-t),P对应的数是-(10-2t),
当P在Q的左边时,[-(7-t)]-[-(10-2t)]=2,
解得:t=1
当P在Q的左边时,[-(10-2t)]-[-(7-t)]=2,
解得:t=5,
即当1秒或5秒后,P、Q两点间的距离为2.
故答案为:t=1或5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位要制作一批宣传材料.甲公司提出:每份材料收费1元,另收取制版费600元;乙公司提出:每份材料收费1.2元,不收取制版费.
(1)设制作
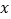 份宣传材料,甲公司收费
份宣传材料,甲公司收费 元,乙公司收费
元,乙公司收费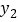 元,请分别写出
元,请分别写出 ,
,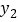 与
与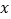 的关系式;
的关系式;(2)该单位要制作宣传材料1000~4500(含1000和4500)份,选择哪家公司比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
(1)乙车的速度为80km/h(千米/小时);(2)a=40,m=1;(3)甲车共行驶了7h;(4)乙车一定行驶了
 h或
h或 h,两车恰好距离50km.
h,两车恰好距离50km.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
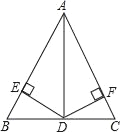
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
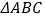 中,点
中,点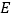 在
在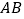 上,点
上,点 在
在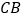 的延长线上,且
的延长线上,且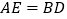 .试探索以下问题:
.试探索以下问题: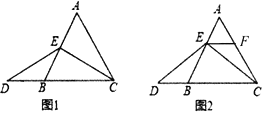
(1)当点
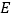 为
为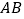 的中点时,如图1,求证:
的中点时,如图1,求证: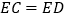 .
.(2)如图2,当点
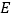 不是
不是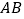 的中点时,过点
的中点时,过点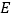 作
作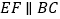 ,交
,交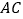 于点
于点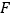 ,求证:
,求证: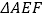 是等边三角形.
是等边三角形.(3)在(2)的条件下,
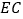 与
与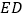 还相等吗?请说明理由.
还相等吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

相关试题

