【题目】在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .试探索以下问题:
.试探索以下问题:
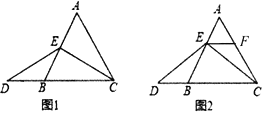
(1)当点![]() 为
为![]() 的中点时,如图1,求证:
的中点时,如图1,求证:![]() .
.
(2)如图2,当点![]() 不是
不是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() 是等边三角形.
是等边三角形.
(3)在(2)的条件下,![]() 与
与![]() 还相等吗?请说明理由.
还相等吗?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)ED=EC.
【解析】
(1)根据等边三角形的性质得出AB=AC=BC,∠ABC=∠ACB=∠A=60°,再由E是AB的中点,AE=BE=BD,证出∠EDB=∠ECB,得出EC=ED;
(2)在△AEF中,只要证明有两个内角是60°即可;
(3)只要证明△DBE≌△EFC,即可推出结论.
解:(1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,
∠ABC=∠ACB=∠A=60o ,
∵E是AB的中点,
∴AE=BE,∠ECB=![]() ∠ACB=30°,
∠ACB=30°,
∵AE=BD,
∴BE=BD,
∴∠EDB=∠DEB=![]() ∠ABC=30°,
∠ABC=30°,
∴∠EDB=∠ECB,
∴EC=ED.
(2)∵EF∥BC,
∴∠AEF=∠ABC=60 o,∠AFE=∠ACB=60°,
∴△AEF是等边三角形,
(3)ED=EC.理由如下:
由(2)得:△AEF是等边三角形
∴∠AFE=∠ABC=60°,AE=EF=AF
∴∠EFC=∠DBE=120°,
又∵AE=BD,AB=AC,
∴BD=EF,BE=FC,
∴△DBE≌△EFC(SAS),
∴ED=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
(1)乙车的速度为80km/h(千米/小时);(2)a=40,m=1;(3)甲车共行驶了7h;(4)乙车一定行驶了
 h或
h或 h,两车恰好距离50km.
h,两车恰好距离50km.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示,设点A,B,C所对应的数的和是
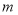 .
.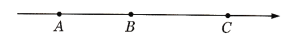
(1)若以点B为原点,则点C所对应的数是 ,若以点C的原点,则
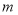 的值是 .
的值是 .(2)若原点O在图中数轴上,且点C到原点的距离为4,求
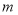 的值.
的值.(3)动点P从点A出发,以每秒2个单位长度的速度向终点C移动,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,
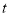 秒后,P,Q两点间距离为2?(请直接写出答案)
秒后,P,Q两点间距离为2?(请直接写出答案)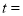 .
. -
科目: 来源: 题型:
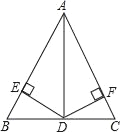
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
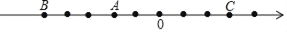
相关试题

