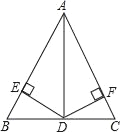
【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据角平分线的性质得到DE=DF,证明Rt△BDE≌Rt△CDF,根据全等三角形的性质得到∠B=∠C,根据等腰三角形的判定定理证明;
(2)根据直角三角形的性质求出AC,根据勾股定理计算即可.
(1)证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BDE和Rt△CDF中,![]() ,
,
∴Rt△BDE≌Rt△CDF,
∴∠B=∠C,
∴AB=AC;
(2)∵AD平分∠BAC,BD=CD,
∴AD⊥BC,
∵∠DAC=30°,
∴AC=2DC=8,
∴AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位要制作一批宣传材料.甲公司提出:每份材料收费1元,另收取制版费600元;乙公司提出:每份材料收费1.2元,不收取制版费.
(1)设制作
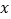 份宣传材料,甲公司收费
份宣传材料,甲公司收费 元,乙公司收费
元,乙公司收费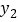 元,请分别写出
元,请分别写出 ,
,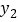 与
与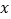 的关系式;
的关系式;(2)该单位要制作宣传材料1000~4500(含1000和4500)份,选择哪家公司比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
(1)乙车的速度为80km/h(千米/小时);(2)a=40,m=1;(3)甲车共行驶了7h;(4)乙车一定行驶了
 h或
h或 h,两车恰好距离50km.
h,两车恰好距离50km.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示,设点A,B,C所对应的数的和是
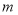 .
.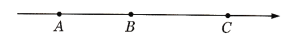
(1)若以点B为原点,则点C所对应的数是 ,若以点C的原点,则
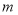 的值是 .
的值是 .(2)若原点O在图中数轴上,且点C到原点的距离为4,求
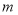 的值.
的值.(3)动点P从点A出发,以每秒2个单位长度的速度向终点C移动,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,
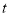 秒后,P,Q两点间距离为2?(请直接写出答案)
秒后,P,Q两点间距离为2?(请直接写出答案)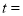 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
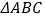 中,点
中,点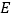 在
在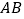 上,点
上,点 在
在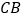 的延长线上,且
的延长线上,且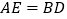 .试探索以下问题:
.试探索以下问题: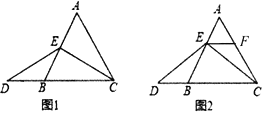
(1)当点
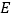 为
为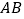 的中点时,如图1,求证:
的中点时,如图1,求证: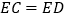 .
.(2)如图2,当点
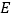 不是
不是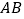 的中点时,过点
的中点时,过点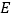 作
作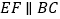 ,交
,交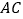 于点
于点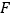 ,求证:
,求证: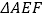 是等边三角形.
是等边三角形.(3)在(2)的条件下,
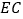 与
与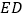 还相等吗?请说明理由.
还相等吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
相关试题

