【题目】如图,在平面直角坐标系中,四边形![]() 为正方形,已知点
为正方形,已知点![]() 、
、![]() ,点
,点![]() 、
、![]() 在第二象限内.
在第二象限内.
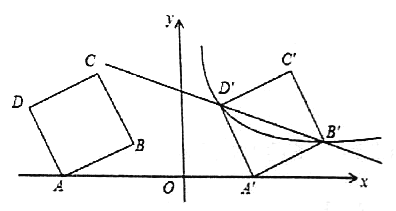
(1)点![]() 的坐标___________;
的坐标___________;
(2)将正方形![]() 以每秒
以每秒![]() 个单位的速度沿
个单位的速度沿![]() 轴向右平移
轴向右平移![]() 秒,若存在某一时刻
秒,若存在某一时刻![]() ,使在第一象限内点
,使在第一象限内点![]() 、
、![]() 两点的对应点
两点的对应点![]() 、
、![]() 正好落在某反比例函数的图象上,请求出此时
正好落在某反比例函数的图象上,请求出此时![]() 的值以及这个反比例函数的解析式;
的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在![]() 轴上的点
轴上的点![]() 和反比例函数图象上的点
和反比例函数图象上的点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点
四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)点![]() 坐标为
坐标为![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,
;(3)存在,![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]()
【解析】
(1)证明△DFA≌△AEB(AAS),则DF=AE=3,BE=AF=1,即可求解;
(2)t秒后,点D′(7+2t,3)、B′(3+2t,1),则k=(7+2t)×3=(3+2t)×1,即可求解;
(3)分![]() 为平行四边形的一条边时和
为平行四边形的一条边时和![]() 为平行四边形对角线时两种情况,分别求解即可.
为平行四边形对角线时两种情况,分别求解即可.
解:(1)过点![]() 、
、![]() 分别作
分别作![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,
,

![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ;
;
(2)![]() 秒后,点
秒后,点![]() 、
、![]() ,
,
则![]() ,解得:
,解得:![]() ,则
,则![]() ,
,![]()
(3)存在,理由:
设:点![]() ,点
,点![]() ,
,![]() ,
,
①![]() 在第一象限,且
在第一象限,且![]() 为平行四边形的一条边时,图示平行四边形
为平行四边形的一条边时,图示平行四边形![]() ,点
,点![]() 向左平移
向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位得到点
个单位得到点![]() ,
,
同理点![]() 向左平移
向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位为
个单位为![]() 得到点
得到点![]() ,即:
,即:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,
故点![]() 、点
、点![]() ;
;
②![]() 在第一象限,且当
在第一象限,且当![]() 为平行四边形对角线时,图示平行四边形
为平行四边形对角线时,图示平行四边形![]() ,
,![]() 中点坐标为
中点坐标为![]() ,
,
该中点也是![]() 的中点,
的中点,
即:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,
故点![]() 、
、![]() ;
;

③![]() 在第三象限,且当
在第三象限,且当![]() 为平行四边形的一条边时,图示平行四边形
为平行四边形的一条边时,图示平行四边形![]() ,点
,点![]() 向左平移
向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位得到点
个单位得到点![]() ,
,
同理点![]() 向右平移
向右平移![]() 个单位、向下平移
个单位、向下平移![]() 个单位为
个单位为![]() 得到点
得到点![]() ,即:
,即:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,
故点![]() 、点
、点![]() ;
;
综上:![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( )

A.伦敦的时间是2020年1月9日凌晨1时
B.纽约的时间是2020年1月9日晚上20时
C.多伦多的时间是2020年1月8日晚上19时
D.汉城的时间是2020年1月9日上午8时
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图(1),
 ,
,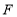 ,
, ,
, 四点分别在四边形
四点分别在四边形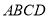 的四条边上,若四边形
的四条边上,若四边形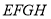 为菱形,我们称菱形
为菱形,我们称菱形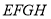 为四边形
为四边形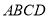 的内接菱形.
的内接菱形.动手操作:

(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由
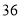 个小正方形组成一个大正方形
个小正方形组成一个大正方形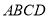 ,点
,点 、
、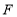 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形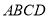 的内接菱形
的内接菱形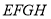 ;
;特例探索:
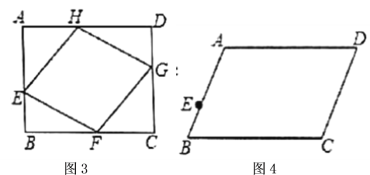
(2)如图3,矩形
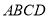 ,
, ,点
,点 在线段
在线段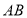 上且
上且 ,四边形
,四边形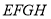 是矩形
是矩形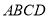 的内接菱形,求
的内接菱形,求 的长度;
的长度;拓展应用:
(3)如图4,平行四边形
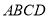 ,
, ,
, ,点
,点 在线段
在线段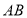 上且
上且 ,
,①请你在图4中画出平行四边形
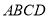 的内接菱形
的内接菱形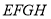 ,点
,点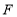 在边
在边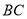 上;
上;②在①的条件下,当
 的长最短时,
的长最短时,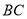 的长为__________
的长为__________ -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:老师所留的作业中有这样一道题,解方程:
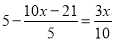 甲、乙两位同学完成的过程如下:
甲、乙两位同学完成的过程如下:
老师发现这两位同学的解答都有错误.
(1)甲同学的解答从第________步开始出现错误;错误的原因是_________________________;乙同学的解答从第_______________步开始出现错误,错误的原因是_________________________;
(2)请重新写出完成此题的正确解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎做一道数学题,“已知两个多项式
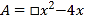 ,
,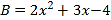 ,试求
,试求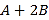 .”其中多项式
.”其中多项式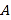 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.(1)小马虎看答案以后知道
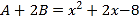 ,请你替小马虎求出系数“
,请你替小马虎求出系数“ ”;
”;(2)在(1)的基础上,小马虎已经将多项式
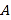 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式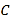 ,要求小马虎求出
,要求小马虎求出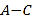 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“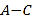 ”看成“
”看成“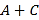 ”,结果求出的答案为
”,结果求出的答案为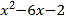 .请你替小马虎求出“
.请你替小马虎求出“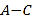 ”的正确答案.
”的正确答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场春节促销活动出售
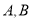 两种商品,活动方案如下两种:
两种商品,活动方案如下两种:方案一
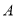
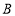
每件标价
90元
100元
每件商品返利
按标价的
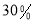
按标价的
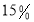
例如买一件
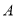 商品,只需付款
商品,只需付款 元
元方案二
所购商品一律按标价20%的返利
(1)某单位购买
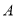 商品
商品 件,
件,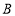 商品20件,选用何种方案划算?
商品20件,选用何种方案划算?(2)某单位购买
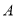 商品件(
商品件(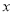 为正整数),购买
为正整数),购买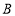 商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少?
商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少?(3)若两种方案的实际付款一样,求
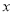 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
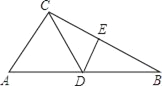
A. 50° B. 65° C. 80° D. 100°
相关试题

