【题目】依次连接菱形的四边中点得到的四边形一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 三角形
参考答案:
【答案】A
【解析】
先连接AC、BD,由于E、H是AB、AD中点,利用三角形中位线定理可知EH∥BD,同理易得FG∥BD,那么有EH∥FG,同理也有EF∥HG,易证四边形EFGH是平行四边形,而四边形ABCD是菱形,利用其性质有AC⊥BD,就有∠AOB=90°,再利用EF∥AC以及EH∥BD,两次利用平行线的性质可得∠HEF=∠BME=90°,即可得证.
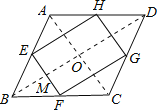
如图:连接AC、BD,相交于点O,
∵E、H是AB、AD中点,
∴EH∥BD,
同理有FG∥BD,
∴EH∥FG,且EH=FG
同理EF∥HG,
∴四边形EFGH是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,
又∵EF∥AC,
∴∠BME=90°,
∵EH∥BD,
∴∠HEF=∠BME=90°,
∴四边形EFGH是矩形.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解八年级学生参加课外体育活动的情况,随机抽取了30名学生,对他们一周内平均每天参加课外体育活动的时间进行了调查,统计结果如下(单位:分):
28,50,40,40,40,53,38,40,34,40,27,21,35,32,40,
40,30,52,35,62,36,15,51,40,38,19,40,40,32,43.
(1)求这组数据的极差;
(2)按组距10分将数据分组,确定每组的组中值,列出频数分布表;
(3)在同一图中画出频数分布直方图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为8,点E为正方形边上一点,连接BE,且BE=10,则AE的长为 .
-
科目: 来源: 题型:
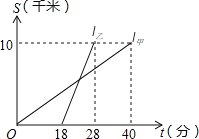
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=
 ,E是BC的中点,AE⊥BD于点F,则CF的长是 .
,E是BC的中点,AE⊥BD于点F,则CF的长是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求三次传球后,球回到甲脚下的概率;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大? -
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意结合图形填空:如图,

点
 在
在 上,点
上,点 在
在 上,
上, ,
,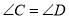 .试说明:
.试说明: ∥
∥ .将过程补充完整.
.将过程补充完整.解:∵
 (已知)
(已知)且
 ( )
( )∴
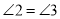 (等量代换)
(等量代换)∴ ∥ ( )
∴
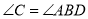 ( )
( )又∵
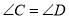 (已知)
(已知)∴ = (等量代换 )
∴
 ∥
∥ ( )
( )
相关试题

