【题目】甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求三次传球后,球回到甲脚下的概率;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
参考答案:
【答案】
(1)
解:根据题意画出树状图如下:
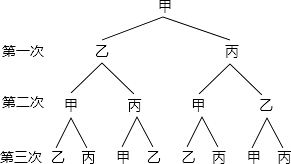
由树形图可知三次传球有8种等可能结果;
三次传球后,球回到甲脚下的概率= ![]() =
= ![]() ;
;
(2)
由(1)可知球回到乙脚下的概率= ![]() ,
,
所以球回到乙脚下的概率大.
【解析】(1)画出树状图,根据树形图,利用概率公式列式求出球回到甲脚下的概率即可得解;(2)计算出传到乙脚下的概率,比较大小即可.
【考点精析】利用列表法与树状图法对题目进行判断即可得到答案,需要熟知当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
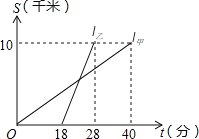
查看答案和解析>>【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】依次连接菱形的四边中点得到的四边形一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=
 ,E是BC的中点,AE⊥BD于点F,则CF的长是 .
,E是BC的中点,AE⊥BD于点F,则CF的长是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意结合图形填空:如图,

点
 在
在 上,点
上,点 在
在 上,
上, ,
,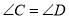 .试说明:
.试说明: ∥
∥ .将过程补充完整.
.将过程补充完整.解:∵
 (已知)
(已知)且
 ( )
( )∴
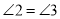 (等量代换)
(等量代换)∴ ∥ ( )
∴
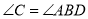 ( )
( )又∵
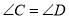 (已知)
(已知)∴ = (等量代换 )
∴
 ∥
∥ ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
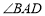 ,点
,点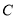 是
是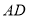 边上的一点,按要求画图,并保留作图痕迹.
边上的一点,按要求画图,并保留作图痕迹.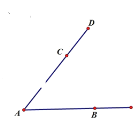
(1)用尺规作图法在
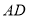 的右侧以点
的右侧以点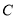 为顶点作
为顶点作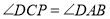 ;
;(2)射线
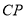 与
与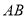 的位置关系是____________,理由是____________.
的位置关系是____________,理由是____________.(3)画出表示点
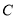 到
到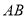 的距离的线段和表示点
的距离的线段和表示点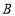 到
到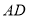 的距离的线段.
的距离的线段. -
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
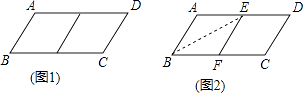
(1)猜想与计算:
邻边长分别为3和5的平行四边形是阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD是阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
相关试题

