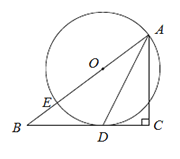
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】试题分析:
(1)连接OD,由⊙O与BC边相切于点D可得∠ODB=∠C=90°,从而可得OD∥AC,由此即可得到∠CAD=∠ADO,由OD=OA可得∠DAO=∠ODA,即可得到∠CAD=∠DAO,从而得到AD是∠BAC的角平分线;
(2)在Rt△ABC中,由AC=3,BC=4易得AB=5,由tanB=![]() ,设OD=3x,则BD=4x,由此在Rt△OBD中可得OB=5x,结合OA=OD=3x可得AB=8x=5,解得x=
,设OD=3x,则BD=4x,由此在Rt△OBD中可得OB=5x,结合OA=OD=3x可得AB=8x=5,解得x=![]() ,即可得到⊙O的半径为:
,即可得到⊙O的半径为: ![]() .
.
试题分析:
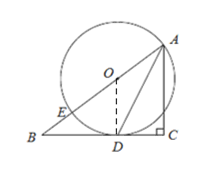
(1)如图,连接OD,
∵⊙O与BC边相切于点D,
∴∠ODB=∠C=90°,
∴OD∥AC,
∴∠CAD=∠ADO,
∵OD=OA,
∴∠DAO=∠ODA,
∴∠CAD=∠DAO,
∴AD是∠BAC的角平分线;
(2)∵在Rt△ABC中,由AC=3,BC=4,
∴AB=![]() ,
,
∵tanB=![]() ,
,
∴可设OD=3x,则BD=4x,
∴OB=![]() ,
,
又∵OA=OD=3x,
∴AB=3x+5x=8x=5,解得:x=![]() ,
,
∴⊙O的半径OD=3x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)

(2)

(3)278(x﹣3)﹣463(6﹣2x)﹣888(7﹣21x)=0
(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 的边长为4,点
的边长为4,点 是△ABC的中心,
是△ABC的中心, ,
, 的两边
的两边 与
与 分别相交于
分别相交于 ,
, 绕
绕 点顺时针旋转时,下列四个结论正确的个数是( )
点顺时针旋转时,下列四个结论正确的个数是( )①
 ;②
;② ;③
;③ ;④
;④ 周长最小值是9.
周长最小值是9.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 O
O 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线 和
和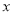 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(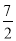 ,
,  ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.
相关试题

