【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
参考答案:
【答案】解:发现:如图2,
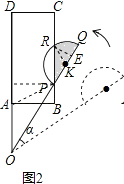
设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,
过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,
∴∠POH=30°,
∴α=60°﹣30°=30°,
∵AD∥BC,
∴∠RPO=∠POH=30°,
∴∠RKQ=2×30°=60°,
∴S扇形KRQ= ![]() =
= ![]() ,
,
在Rt△RKE中,RE=RKsin60°= ![]() ,
,
∴S△PRK= ![]() RE=
RE= ![]() ,
,
∴S阴影= ![]() +
+ ![]() ;
;
拓展:如图5,
∵∠OAN=∠MBN=90°,∠ANO=∠BNM,
∴△AON∽△BMN,
∴ ![]() ,即
,即 ![]() ,
,
∴BN= ![]() ,
,
如图4,
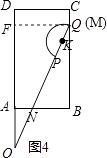
当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF= ![]() ﹣AO=2
﹣AO=2 ![]() ﹣1,
﹣1,
∴x的取值范围是0<x≤2 ![]() ﹣1;
﹣1;
探究:半圆K与矩形ABCD的边相切,分三种情况;
①如图5,
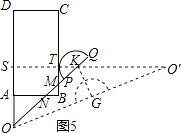
半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,
则∠KSO=∠KTB=90°,
作KG⊥OO′于G,在Rt△OSK中,
OS= ![]() =2,
=2,
在Rt△OSO′中,SO′=OStan60°=2 ![]() ,KO′=2
,KO′=2 ![]() ﹣
﹣ ![]() ,
,
在Rt△KGO′中,∠O′=30°,
∴KG= ![]() KO′=
KO′= ![]() ﹣
﹣ ![]() ,
,
∴在Rt△OGK中,sinα= ![]() =
= ![]() =
= ![]() ,
,
②当半圆K与AD相切于T,如图6,
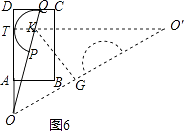
同理可得sinα= ![]() =
= ![]() =
= 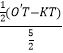 =
= ![]() ;
;
③当半圆K与CD切线时,点Q与点D重合,且为切点,
∴α=60°,
∴sinα=sin60°= ![]() ;
;
综上所述sinα的值为: ![]() 或
或 ![]() 或
或 ![]()
【解析】首先设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,根据直角三角形的直角边与斜边的关系得出∠POH=30° ;进而求得α的度数,根据平行线的性质及圆周角定理得出∠RKQ的度数,然后利用S阴影=S扇形KRQ+S△PRK求得答案;
拓展:如图5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN,根据相似三角形对应边成比例即可求得BN,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,根据勾股定理求出BQ=AF的值,则可求出x的取值范围;
探究:半圆K与矩形ABCD的边相切,分三种情况:①半圆K与BC相切于点T,②当半圆K与AD相切于T,③当半圆K与CD切线时,点Q与点D重合,且为切点;分别求解即可求得答案.
-
科目: 来源: 题型:
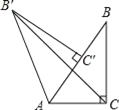
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为
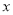 (千克),在甲采摘园所需总费用为
(千克),在甲采摘园所需总费用为 (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为 (元).
(元).(1)当采摘量超过10千克时,求
 与
与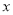 的关系式;
的关系式;(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.

(1)写出点A,B,C,D的坐标;
(2)求点A和点C之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO=
 .
.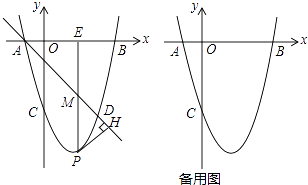
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
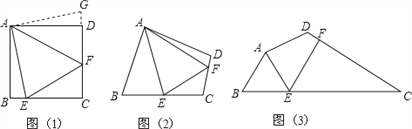
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(
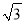 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: 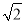 =1.41,
=1.41, 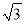 =1.73)
=1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=
 AD时(如图2):
AD时(如图2):∵AP=
 AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,∴S△ABP=
 S△ABD,
S△ABD,∵PD=AD﹣AP=
 AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等∴S△CDP=
 S△CDA,
S△CDA,∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣
 S△ABD﹣
S△ABD﹣ S△CDA,
S△CDA,=S四边形ABCD﹣
 (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣ (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)= S△DBC+
S△DBC+ S△ABC.
S△ABC.(1)当AP=
 AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;(2)当AP=
 AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;(3)一般地,当AP=
 AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;(4)当AP=
 AD(0≤
AD(0≤ ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
相关试题

