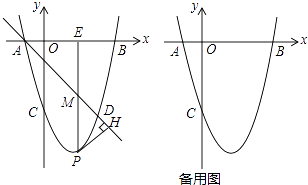
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO= ![]() .
.
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)解:∵点A的坐标为(﹣1,0),
∴OA=1.
又∵tan∠ACO= ![]() ,
,
∴OC=4.
∴C(0,﹣4).
∵OC=OB,
∴OB=4
∴B(4,0).
设抛物线的解析式为y=a(x+1)(x﹣4).
∵将x=0,y=﹣4代入得:﹣4a=﹣4,解得a=1,
∴抛物线的解析式为y=x2﹣3x﹣4
(2)解:∵抛物线的对称轴为x=﹣ ![]() =
= ![]() ,C(0,﹣4),点D和点C关于抛物线的对称轴对称,
,C(0,﹣4),点D和点C关于抛物线的对称轴对称,
∴D(3,﹣4).
设直线AD的解析式为y=kx+b.
∵将A(﹣1,0)、D(3,﹣4)代入得: ![]() ,解得k=﹣1,b=﹣1,
,解得k=﹣1,b=﹣1,
∴直线AD的解析式y=﹣x﹣1.
∵直线AD的一次项系数k=﹣1,
∴∠BAD=45°.
∵PM平行于y轴,
∴∠AEP=90°.
∴∠PMH=∠AME=45°.
∴△MPH的周长=PM+MH+PH=PM+ ![]() MP+
MP+ ![]() PM=(1+
PM=(1+ ![]() )PM.
)PM.
设P(a,a2﹣3a﹣4),M(﹣a﹣1),则PM=﹣a﹣1﹣(a2﹣3a﹣4)=﹣a2+2a+3,
∵PM=﹣a2+2a+3=﹣(a﹣1)2+4,
∴当a=1时,PM有最大值,最大值为4.
∴△MPH的周长的最大值=4×(1+ ![]() )=4+4
)=4+4 ![]()
(3)解:如图1所示;当∠EGN=90°.
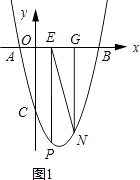
设点G的坐标为(a,0),则N(a,a2﹣3a﹣4).
∵∠EGN=∠AOC=90°,
∴ ![]() 时,△AOC∽△EGN.
时,△AOC∽△EGN.
∴ ![]() =
= ![]() ,整理得:a2+a﹣8=0.
,整理得:a2+a﹣8=0.
解得:a= ![]() (负值已舍去).
(负值已舍去).
∴点G的坐标为( ![]() ,0).
,0).
如图2所示:当∠EGN=90°.
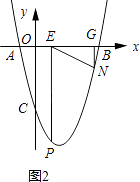
设点G的坐标为(a,0),则N(a,a2﹣3a﹣4).
∵∠EGN=∠AOC=90°,
∴ ![]() 时,△AOC∽△NGE.
时,△AOC∽△NGE.
∴ ![]() =4,整理得:4a2﹣11a﹣17=0.
=4,整理得:4a2﹣11a﹣17=0.
解得:a= ![]() (负值已舍去).
(负值已舍去).
∴点G的坐标为( ![]() ,0).
,0).
∵EN在EP的右面,
∴∠NEG<90°.
如图3所示:当∠ENG′=90°时,
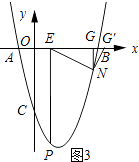
EG′=EG× ![]() ×
× ![]() =(
=( ![]() ﹣1)×
﹣1)× ![]() =
= ![]() .
.
∴点G′的横坐标= ![]() .
.
∵ ![]() ≈4.03>4,
≈4.03>4,
∴点G′不在EG上.
故此种情况不成立.
综上所述,点G的坐标为( ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)先由锐角三角函数的定义求得C的坐标,从而得到点B的坐标,设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入求解即可;
(2)先求得抛物线的对称轴,从而得到点D(3,-4),然后利用待定系数法可求得直线AD的解析式,根据直线AD的一次项系数的特点得出∠BAD=45°,进而得出△PMD为等腰直角三角形,所当PM有最大值时三角形的周长最大,设P(a,a2-3a-4),M(-a-1),则PM=-a2+2a+3,然后利用配方可求得PM的最大值,最后根据△MPH的周长=(![]() )PM,即可以得出答案;
)PM,即可以得出答案;
(3)当∠EGN=90°时,设点G的坐标为(a,0),则N(a,a2-3a-4),则EG=a-1,NG=-a2+3a+4,故OA∶OC=EG∶GN ;如果△AOC∽△EGN,然后根据题意列方程求解判断是否适合题意即可 。’
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和二次函数的最值的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为
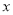 (千克),在甲采摘园所需总费用为
(千克),在甲采摘园所需总费用为 (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为 (元).
(元).(1)当采摘量超过10千克时,求
 与
与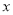 的关系式;
的关系式;(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.

(1)写出点A,B,C,D的坐标;
(2)求点A和点C之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).

发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
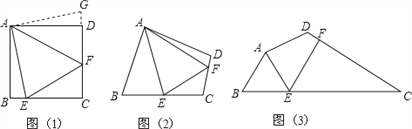
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(
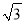 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: 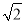 =1.41,
=1.41, 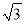 =1.73)
=1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=
 AD时(如图2):
AD时(如图2):∵AP=
 AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,∴S△ABP=
 S△ABD,
S△ABD,∵PD=AD﹣AP=
 AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等∴S△CDP=
 S△CDA,
S△CDA,∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣
 S△ABD﹣
S△ABD﹣ S△CDA,
S△CDA,=S四边形ABCD﹣
 (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣ (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)= S△DBC+
S△DBC+ S△ABC.
S△ABC.(1)当AP=
 AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;(2)当AP=
 AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;(3)一般地,当AP=
 AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;(4)当AP=
 AD(0≤
AD(0≤ ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角梯形
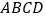 中,
中, ,
, 为
为 边上一点,
边上一点, ,且
,且 .连接
.连接 交对角线
交对角线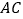 于
于 ,连接
,连接 .下列结论:
.下列结论:
①
 ;②
;② 为等边三角形;
为等边三角形;③
 ; ④
; ④ .其中结论正确的是
.其中结论正确的是A.只有①②
B.只有①②④
C.只有③④
D.①②③④
相关试题

