搜索
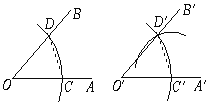
【题目】用直尺和圆规画一个角等于已知角，是运用了“全等三角形的对应角相等”这一性质，其全等的依据是（ ）
A．SAS B．ASA C．AAS D．SSS
参考答案：
【答案】D
【解析】
试题本题考查的关键是作角的过程，作角过程中所产生的条件就是证明全等的条件．根据用直尺和圆规画一个角等于已知角的过程很容易看出所得两个三角形三边对应相等．
解：设已知角为∠O，以顶点O为圆心，任意长为半径画弧，交角的两边分别为A，B两点；
画一条射线b，端点为M；
以M为圆心，OA长为半径画弧，交射线b于C点；以C为圆心，AB长为半径画弧，两弧交于点D；
作射线MD．
则∠COD就是所求的角．
由以上过程不难看出两个三角形中有三条边对应相等，
∴证明全等的方法是SSS．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知矩形OABC中，OA=2，AB=4，双曲线
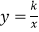（k＞0）与矩形两边AB、BC分别交于E、F．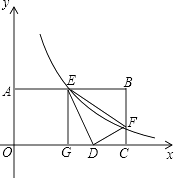
（1）若E是AB的中点，求F点的坐标；
（2）若将△BEF沿直线EF对折，B点落在x轴上的D点，作EG⊥OC，垂足为G，证明△EGD∽△DCF，并求k的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解九年级学生体育测试情况，以九年级（1）班学生的体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：
（说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）
（1）请把条形统计图补充完整；
（2）扇形统计图中D级所在的扇形的圆心角度数是多少？
（3）若该校九年级有600名学生，请用样本估计体育测试中A级学生人数约为多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】“低碳生活，绿色出行”，自行车正逐渐成为人们喜爱的交通工具．某运动商城的自行车销售量自2013年起逐月增加，据统计，该商城1月份销售自行车64辆，3月份销售了100辆．
（1）若该商城前4个月的自行车销量的月平均增长率相同，问该商城4月份卖出多少辆自行车？
（2）考虑到自行车需求不断增加，该商城准备投入3万元再购进一批两种规格的自行车，已知A型车的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆．根据销售经验，A型车不少于B型车的2倍，但不超过B型车的2.8倍．假设所进车辆全部售完，为使利润最大，该商城应如何进货？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，BP是△ABC中∠ABC的平分线，CP是△ABC的外角∠ACM的平分线，如果∠ABP＝20°，∠ACP＝50°，那么∠A＋∠P的度数为( )
A. 60° B. 70° C. 80° D. 90°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c的图象的顶点C的坐标为（0，﹣2），交x轴于A、B两点，其中A（﹣1，0），直线l：x=m（m＞1）与x轴交于D．
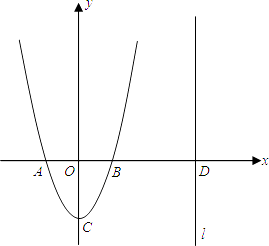
（1）求二次函数的解析式和B的坐标；
（2）在直线l上找点P（P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求点P的坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，在抛物线上是否存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形？如果存在，请求出点Q的坐标；如果不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心．重心有很多美妙的性质，如关于线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题．请你利用重心的概念完成如下问题：
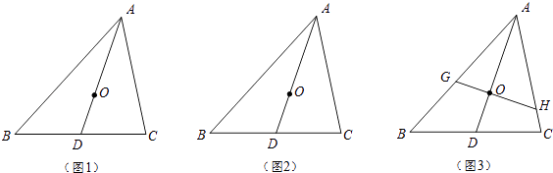
（1）若O是△ABC的重心（如图1），连结AO并延长交BC于D，证明：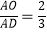
；
（2）若AD是△ABC的一条中线（如图2），O是AD上一点，且满足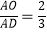 ，试判断O是△ABC的重心吗？如果是，请证明；如果不是，请说明理由；
（3）若O是△ABC的重心，过O的一条直线分别与AB、AC相交于G、H（均不与△ABC的顶点重合）（如图3），S四边形BCHG ， S△AGH分别表示四边形BCHG和△AGH的面积，试探究
的最大值．
相关试题
