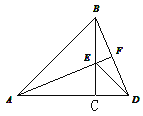
【题目】在△ABC和△DEC中,∠ACB=∠ECD=90°,AC=BC=12,DC=EC=5.当点A.C、D在同一条直线上时,AF的长度为_______.
参考答案:
【答案】![]()
【解析】分析:先根据AC=BC, ∠ACB=∠ECD=90°,DC=EC,可证明Rt△ACE≌Rt△BCD,
根据全等三角形性质可得∠EAD=∠CBD,根据∠EAD+∠AEC =90°, ∠CEA=∠BEF,可证得: ∠CBD+∠BEF=90°,继而可得: ∠BFA=90°,所以AF⊥BD,然后在Rt△BCD中,根据勾股定理可得:BD=![]() ,最后根据等面积法可得:
,最后根据等面积法可得:![]() ,代入数值即可求解.
,代入数值即可求解.
详解: 因为AC=BC, ∠ACB=∠ECD=90°,DC=EC,
所以Rt△ACE≌Rt△BCD,
所以∠EAD=∠CBD,
因为∠EAD+∠AEC =90°, ∠CEA=∠BEF,
所以 ∠CBD+∠BEF=90°,
所以 ∠BFA=90°,
所以AF⊥BD,
在Rt△BCD中,根据勾股定理可得:BD=![]() ,
,
由等面积法可得:![]() ,
,
所以![]() ,
,
所以![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
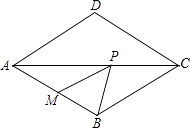
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( )
A.6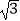
B.3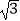
C.9
D.4.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与双曲线y=
x与双曲线y= 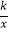 (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= 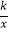 (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3
 m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3 m,则鱼竿转过的角度是__________.
m,则鱼竿转过的角度是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=8
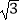 ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 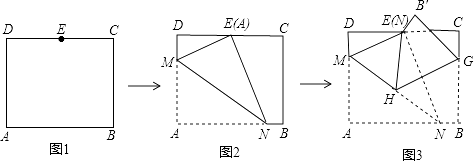
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
相关试题

