【题目】如图1,在矩形纸片ABCD中,AB=8 ![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 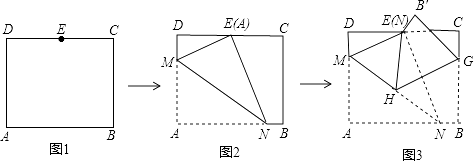
参考答案:
【答案】![]()
![]()
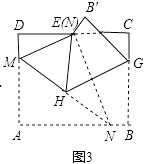
【解析】解:如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x, ∵DE=EC,AB=CD=8 ![]() ,
,
∴DE= ![]() CD=4
CD=4 ![]() ,
,
在RT△DEM中,∵DM2+DE2=EM2 ,
∴(4 ![]() )2+x2=(10﹣x)2 ,
)2+x2=(10﹣x)2 ,
解得x=2.6,
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,
∴∠DEM=∠ENF,∵∠D=∠EFN=90°,
∴△DME∽△FEN,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EN= ![]()
![]() ,
,
∴AN=EN= ![]()
![]() ,
,
∴tan∠AMN= ![]() =
= ![]()
![]() ,
,
如图3中,∵ME⊥EN,HG⊥EN,
∴EM∥GH,
∴∠NME=∠NHG,
∵∠NME=∠AMN,∠EHG=∠NHG,
∴∠AMN=∠EHG,
∴tan∠EHG=tan∠AMN= ![]()
![]() .
.
方法二,tan∠EHG=tan∠EMN= ![]() =
= ![]() .
.
故答案为 ![]()
![]() .
.
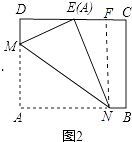
如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x,利用勾股定理求出x,再利用△DME∽△FEN,得 ![]() =
= ![]() ,求出EN,EM,求出tan∠AMN,再证明∠EHG=∠AMN即可解决问题.
,求出EN,EM,求出tan∠AMN,再证明∠EHG=∠AMN即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是 .

-
科目: 来源: 题型:
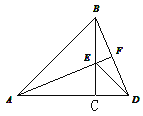
查看答案和解析>>【题目】在△ABC和△DEC中,∠ACB=∠ECD=90°,AC=BC=12,DC=EC=5.当点A.C、D在同一条直线上时,AF的长度为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3
 m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3 m,则鱼竿转过的角度是__________.
m,则鱼竿转过的角度是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的有( )个
①绝对值相等的两数相等.②若a,b互为相反数,则
 =﹣1.③如果a大于b,那么a的倒数小于b的倒数.④任意有理数都可以用数轴上的点来表示.⑤x2﹣2x﹣33x3+25是五次四项.⑥两个负数比较大小,绝对值大的反而小.⑦一个数的相反数一定小于或等于这个数.⑧正数的任何次幂都是正数,负数的任何次幂都是负数.
=﹣1.③如果a大于b,那么a的倒数小于b的倒数.④任意有理数都可以用数轴上的点来表示.⑤x2﹣2x﹣33x3+25是五次四项.⑥两个负数比较大小,绝对值大的反而小.⑦一个数的相反数一定小于或等于这个数.⑧正数的任何次幂都是正数,负数的任何次幂都是负数.A. 4个 B. 5个 C. 6个 D. 7个
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

相关试题

