【题目】已知点![]() 在直线
在直线![]() 上,
上,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
![]()
(1)如图,点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,求线段
,求线段![]() 的长;
的长;
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长;
的长;
参考答案:
【答案】(1)![]() ;(2)①若点
;(2)①若点![]() 在线段
在线段![]() 上,
上,![]() ;②若点
;②若点![]() 在
在![]() 的延长线上,
的延长线上,![]() ;③若点
;③若点![]() 在
在![]() 的延长线上,
的延长线上,![]() .
.
【解析】
(1)由线段中点的定义以及AC的长度可求得CM的长,再由![]() 以及BC的长可求得CN的长,继而根据MN=MC+NC即可求得答案;
以及BC的长可求得CN的长,继而根据MN=MC+NC即可求得答案;
(2)分点C在线段AB上,在AB的延长线上和在BA的延长线上三种情况分别求解即可得.
(1)因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,且
,且![]() ,
,
所以![]() .
.
所以![]() .
.
(2)①若点![]() 在线段
在线段![]() 上,
上,
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,且
,且![]() ,
,![]() ,
,
所以![]() ,
,
所以![]()
![]() ;
;
②若点![]() 在
在![]() 的延长线上,如图
的延长线上,如图
![]()
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,且
,且![]() ,
,![]() ,
,
所以![]() ,
,
所以![]()
![]() ;
;
③若点![]() 在
在![]() 的延长线上,如图
的延长线上,如图
![]()
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,且
,且![]() ,
,![]() ,
,
所以![]() ,
,
所以![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,
组别
分数段(分)
频数
频率
A组
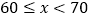
30
0.1
B组

90
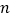
C组
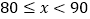
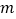
0.4
D组
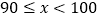
60
0.2
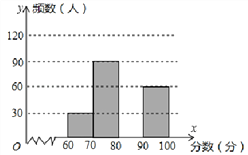
请根据图表信息解答下列问题:
(1)在表中:
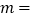 ,
,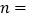 ;
;(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】早在1960年、中国登山队首次从珠穆朗玛北侧中国境内登上珠峰,近几十年,珠峰更是吸引了大批的登山爱好者,某日,登山运动员傅博准备从海拔7400米的3号营地登至海拔近7900米的4号营地,由于天气骤变,近6小时的攀爬过程中他不得不几次下撤躲避强高空风,记向上爬升的海拔高度为正数,向下撒退时下降的海拔高度为负数,傅博在这一天攀爬的海拔高度记录如下:(单位:米)+320、-55、+116、-20、+81、-43、+115.
(1)傳博能按原计划在这天登至4号营地吗?
(2)若在这一登山过程中,傅博所处位置的海拔高度上升或下降1米平均消耗8大卡的卡路里,则傅博这天消耗了多少卡路里?
(3)登山消耗的卡路里预估为:1千克身体重量(体重或负重)1天需要55~65(大于等于55,小于等于65)大卡的卡路里,海拔6000米以上会使卡路里消耗增加20%,登山协会约定海拔5000米以上运动员负重14千克,在(2)的条件下,请你估算傳博的体重范围.(精确到1千克)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一拱桥的截面呈抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,拱桥与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m景观灯.
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我县盛产不知火和脐橙两种水果 ,某公司计划用两种型号的汽车运输不知火和脐橙到外地销售,运输中要求每辆汽车都要满载满运,且只能装运一种水果.若用3辆汽车装运不知火,2辆汽车装运脐橙可共装载33吨,若用2辆汽车装运不知火,3辆汽车装运脐橙可共装载32吨.
(1)求每辆汽车可装载不知火或脐橙各多少吨?
(2)据调查,全部销售完后,每吨不知火可获利700元,每吨脐橙可获利500元,计划用20辆汽车运输,且脐橙不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在
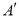 处,BC为折痕。
处,BC为折痕。(1)图①中,若∠1=30°,求∠
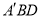 的度数;
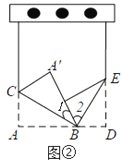
的度数;(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠
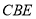 的度数;
的度数;(3)如果在图②中改变∠1的大小,则
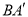 的位置也随之改变,那么问题(2)中∠
的位置也随之改变,那么问题(2)中∠ 的大小是否改变?请说明理由。
的大小是否改变?请说明理由。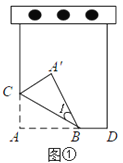
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,
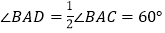 ,于是
,于是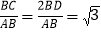 .
.迁移应用
(1)如图2,△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=120°,D,E,C三点在同一直线上,连接BD.
(ⅰ)求证:△ADB≌△AEC;
(ⅱ)请直接写出线段AD,BD,CD之间的等量关系式.
拓展延伸
(2)如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(ⅰ)证明:△CEF是等边三角形;
(ⅱ)若AE=5,CE=2,求BF的长.

相关试题

