【题目】问题背景
如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,
![]() ,于是
,于是![]() .
.
迁移应用
(1)如图2,△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=120°,D,E,C三点在同一直线上,连接BD.
(ⅰ)求证:△ADB≌△AEC;
(ⅱ)请直接写出线段AD,BD,CD之间的等量关系式.
拓展延伸
(2)如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(ⅰ)证明:△CEF是等边三角形;
(ⅱ)若AE=5,CE=2,求BF的长.

参考答案:
【答案】(1)证明见解析(2)3![]()
【解析】分析:![]() (ⅰ)根据
(ⅰ)根据![]() ,得到
,得到![]() ,又
,又![]() ,即可证明.
,即可证明.
(ⅱ)根据![]() ≌
≌![]() ,得到
,得到![]() 借助问题背景的结论得到
借助问题背景的结论得到![]()
根据![]() 即可写出线段AD,BD,CD之间的等量关系式.
即可写出线段AD,BD,CD之间的等量关系式.
![]() (ⅰ)连接BE.根据有一个角等于
(ⅰ)连接BE.根据有一个角等于![]() 的等腰三角形是等边三角形证明即可.
的等腰三角形是等边三角形证明即可.
(ⅱ)如图3,过点B作BH⊥AF于H, AE=5,EF=EC=2,得到FH=4.5,根据![]() , 即可求出BF的长.
, 即可求出BF的长.
详解:(1)(ⅰ)如图,∵![]() ,
,![]() ≌
≌![]() .
.

∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵
∴![]() ≌
≌![]() .
.
(ⅱ)![]() ≌
≌![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .
.
(2)(ⅰ)连接BE.如图3,

∵E、C关于BM对称,
∴![]() 设
设![]() ,则
,则![]() ,
,
![]() .
.
∵![]()
∴![]()
![]()
∴![]() ,
,
又∵![]()
∴△CEF是等边三角形
(ⅱ)如图3,过点B作BH⊥AF于H
∵AE=5,EF=EC=2,
∴FH=4.5,
在Rt△BHF中,
∵∠BFH=30°,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
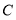 在直线
在直线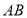 上,
上,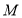 是
是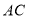 的中点,点
的中点,点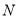 在线段
在线段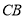 上,且
上,且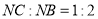 .
.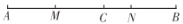
(1)如图,点
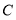 在线段
在线段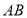 上,若
上,若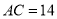 ,
,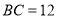 ,求线段
,求线段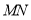 的长;
的长;(2)若
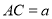 ,
,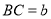 ,求线段
,求线段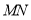 的长;
的长; -
科目: 来源: 题型:
查看答案和解析>>【题目】我县盛产不知火和脐橙两种水果 ,某公司计划用两种型号的汽车运输不知火和脐橙到外地销售,运输中要求每辆汽车都要满载满运,且只能装运一种水果.若用3辆汽车装运不知火,2辆汽车装运脐橙可共装载33吨,若用2辆汽车装运不知火,3辆汽车装运脐橙可共装载32吨.
(1)求每辆汽车可装载不知火或脐橙各多少吨?
(2)据调查,全部销售完后,每吨不知火可获利700元,每吨脐橙可获利500元,计划用20辆汽车运输,且脐橙不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在
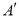 处,BC为折痕。
处,BC为折痕。(1)图①中,若∠1=30°,求∠
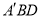 的度数;
的度数;(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠
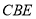 的度数;
的度数;(3)如果在图②中改变∠1的大小,则
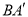 的位置也随之改变,那么问题(2)中∠
的位置也随之改变,那么问题(2)中∠ 的大小是否改变?请说明理由。
的大小是否改变?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,点M、N分别在AD,BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1) -20+(-18)-12 +10
(2)

(3)

(4)(-81)÷2
 ×(-
×(- )÷(-16)
)÷(-16)(5) (-36) ÷4-5×(-1.2)
(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆警车沿着一条南北方向的公路巡视,某天早晨从
 地出发,晚上到达
地出发,晚上到达 地,约定向北为正方向,当天行驶记录如下(单位:千米):
地,约定向北为正方向,当天行驶记录如下(单位:千米): ,
, ,
, ,
, ,
, ,
, ,
, ,
,
(1)问
 地在
地在 地的哪个方向?相距多少千米?
地的哪个方向?相距多少千米?(2)若警车出发时邮箱里剩油18升,该警车每小时耗油0.2升,请问警车在到达B地之前是否需要加油?若需要,至少加多少升油?
相关试题

