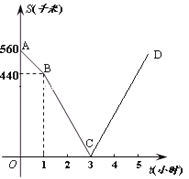
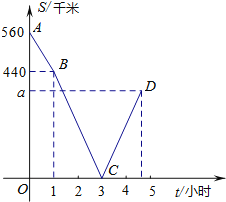
【题目】甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车才出发,并以各自速度匀速行驶,甲车出发3小时两车相遇,相遇后两车仍按原速度原方向各自行驶.如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间![]() (小时)之间的函数图象.则:
(小时)之间的函数图象.则:
①M、N两地之间的距离为________________千米;
②当![]() 时,
时,![]() __________________小时.
__________________小时.
参考答案:
【答案】560 ![]() 或
或![]() .
.
【解析】
(1)根据图象,甲出发时的S值即为M、N两地间的距离;(2)设D点表示甲车到达N地,a表示甲车到达D点时与乙车的距离,先求出甲车的速度,然后设乙车的速度为xkm/h,再利用相遇问题列出方程求解即可;然后求出相遇后甲车到达N地的时间,再根据路程=速度×时间求出两车的相距距离a,即可求出D点坐标,设直线BC的解析式为S=k1t+b1(k1≠0),利用待定系数法求出直线BC的解析式,再令S=50,求出t的值;设直线CD的解析式为S=k2t+b2(k2≠0),利用待定系数法求出直线CD的解析式,再令S=50,求出t的值,进而得出答案.
(1)∵t=0时,S=560,
∴M、N两地的距离为560千米
(2)甲车的速度为:(560-440)÷1=120km/h,
设乙车的速度为xkm/h,
则(120+x)×(3-1)=440,
解得x=100;
相遇后甲车到达N地的时间为:(3-1)×100÷120=![]() (小时),
(小时),
∴a=(120+100)×![]() =
=![]() 千米;
千米;
∴点D的横坐标为![]() +3=
+3=![]() ,即D点坐标为(
,即D点坐标为(![]() ,
,![]() ),
),
设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,![]() ,
,
解得:k1=-220,b1=660,
所以,S=-220t+660,
当-220t+660=50时,解得:t=![]() ,
,
设直线CD的解析式为S=k2t+b2(k2≠0),
将C(3,0),D(![]() ,
,![]() )代入得:
)代入得: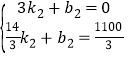 ,
,
解得:k2=220,b2=-660,
所以,S=220t-660(3≤t≤![]() )
)
当220t-660=50时,解得t=![]() ,
,
故答案为:①560;②![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为边BC上的一点,连接AD,过点C作AD的垂线,交过点B与边AC平行的直线于点E,CE交边AB于点F.
(1)求∠EBF的度数;
(2)求证:△ACD≌△CBE;
(3)若AD平分∠BAC,判断△BEF的形状,并说明理由.

-
科目: 来源: 题型:
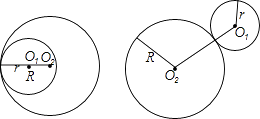
查看答案和解析>>【题目】如果两个圆只有一个公共点,那么我们称这两个圆相切,这个公共点就叫做切点,当两圆相切时,如果其中一个圆(除切点外)在另一个圆的内部,叫做这两个圆内切;其中一个圆(除切点外)在另一个圆的外部,叫做这两个圆外切.如图所示:两圆的半径分别为R,r(R>r),两圆的圆心之间的距离为d,若两个圆外切则d=R+r,若两个圆内切则d=R﹣r,已知两圆的半径分别为方程x2+mx+3=0的两个根,当两圆相切时,已知这两个圆的圆心之间的距离为4,则m的值为 .
-
科目: 来源: 题型:
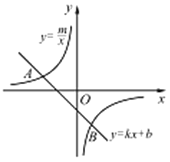
查看答案和解析>>【题目】已知A(-2,1)、B(n,-2)是一次函数y=kx+b的图象与反比例函数y=
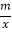 的图象的两个交点.
的图象的两个交点.(1) 求此反比例函数和一次函数的解析式;
(2) 根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用规定的方法解方程:
(1)x2﹣x﹣2=0;(公式法)
(2)x2﹣7=﹣6x.(配方法)
相关试题

