【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表 | |||||
项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
人数 | a | 6 | 5 | 7 | 6 |
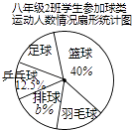
根据图中提供的信息,解答下列问题:
(1)a= , b=;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
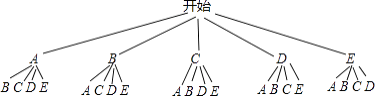
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
参考答案:
【答案】
(1)16;17.5
(2)90
(3)
解:如图,∵共有20种等可能的结果,两名同学恰为一男一女的有12种情况,
∴则P(恰好选到一男一女)= ![]() =
= ![]() .
.
【解析】解:(1)a=5÷12.5%×40%=16,5÷12.5%=7÷b%,
∴b=17.5,
故答案为:16,17.5;
(2)解:600×[6÷(5÷12.5%)]=90(人),
故答案为:90;
(1)首先求得总人数,然后根据百分比的定义求解;(2)利用总数乘以对应的百分比即可求解;(3)利用列举法,根据概率公式即可求解.
-
科目: 来源: 题型:
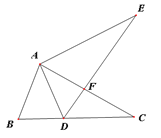
查看答案和解析>>【题目】如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,∠BAD=∠CAE,AC=AE.
(1)求证:△ABC≌△ADE;
(2)若∠B=60°,求证:△ABD是等边三角形.
-
科目: 来源: 题型:
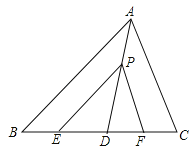
查看答案和解析>>【题目】如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,∠PFD=∠C,点D到AB和AC的距离相等.求证:点D到PE和PF的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一扇窗户,窗框为铝合金材料,下面是由两个大小相等的长方形窗框构成,上面是由三个大小相等的扇形组成的半圆窗框构成,窗户半圆部分安装彩色玻璃,两个长方形部分安装透明玻璃(本题中π取3,长度单位为米).
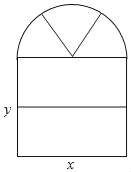
(1)一扇这样窗户一共需要铝合金多少米?(用含x,y的代数式表示)
(2)一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含x,y的代数式表示)
(3)某公司需要购进20扇窗户,在同等质量的前提下,甲、乙两个厂商分别给出如下报价:
铝合金(米/元)
彩色玻璃(平方米/元)
透明玻璃(平方米/元)
甲厂商
200
80
不超过100平方米的部分,90元/平方米,超过100平方米的部分,70元/平方米
乙厂商
220
60
80元/平方米,每购1平方米透明玻璃送0.1米铝合金
当x=2,y=3时,该公司在哪家厂商购买窗户合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)小明做作业时,不小心将方程中
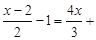 ●的一个常数污染了看不清楚,怎么办呢?
●的一个常数污染了看不清楚,怎么办呢?(1)小红告诉他该方程的解是x=3.那么这个常数应是多少呢?
(2)小芳告诉他该方程的解是负数,并且这个常数是负整数,请你试求该方程的解.(友情提醒:设这个常数为m.)
-
科目: 来源: 题型:
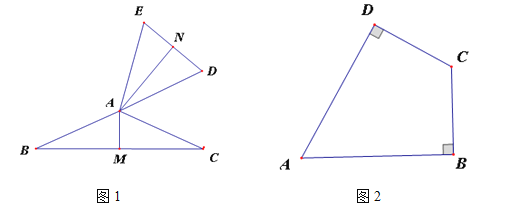
查看答案和解析>>【题目】定义:如果两个等腰三角形的顶角互补,顶角的顶点又是同一个点,而且它们的腰也分别相等,则称这两个三角形互为“顶补等腰三角形”.
(1)如图1,若△ABC与△ADE互为“顶补等腰三角形”.∠BAC>90°,AM⊥BC于M,AN⊥ED于N.求证:DE=2AM;
(2)如图2,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,在四边形ABCD的内部是否存在点P,使得△PAD与△PBC互为“顶补等腰三角形”?若存在,请给予证明,若不存在,请说明理由.
相关试题

