【题目】定义:如果两个等腰三角形的顶角互补,顶角的顶点又是同一个点,而且它们的腰也分别相等,则称这两个三角形互为“顶补等腰三角形”.
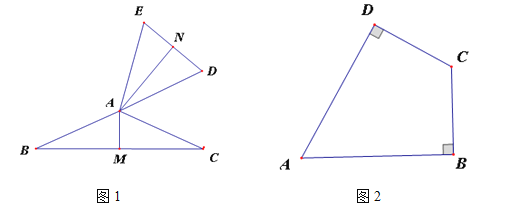
(1)如图1,若△ABC与△ADE互为“顶补等腰三角形”.∠BAC>90°,AM⊥BC于M,AN⊥ED于N.求证:DE=2AM;
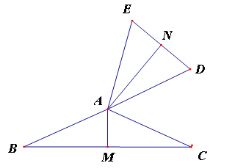
(2)如图2,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,在四边形ABCD的内部是否存在点P,使得△PAD与△PBC互为“顶补等腰三角形”?若存在,请给予证明,若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)存在,证明见解析
【解析】
(1)证明△ABM≌△DAN,由全等三角形的性质得到AM=ND,再由等腰三角形三线合一即可得到结论;
(2)连接AC,取AC的中点P,连接PB,PD.证明点P满足条件即可.
(1)∵△ABC与△ADE互为“顶补等腰三角形”,∴AB=AC=AD=AE,∠BAC+∠DAE=180°,∴∠B=∠C.
又∵AM⊥BC,AN⊥ED,∴∠BMA=∠DNA=90°,∠EAN=∠DAN,DE=2DN,∴∠BAC+2∠NAD=180°.
又∵∠BAC+2∠B=180°,∴∠B=∠NAD.
在△ABM和△DAN中,∵∠BMA=∠DNA=90°,∠B=∠NAD,AB=AD,∴△ABM≌△DAN(AAS),∴AM=DN.
∵AE=AD,AN⊥ED,∴ED=2ND,∴DE=2AM.
(2)存在.
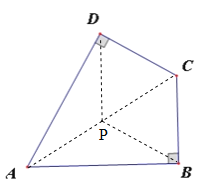
如图,连接AC,取AC的中点P,连接PB,PD.
∵AD=AB,CD=BC,AC=AC,∴△ADC≌△ABC,∴∠ABC=∠ADC=90°.
P是AC的中点,∴PB=PA=PC=![]() AC,PD=PA=PC=
AC,PD=PA=PC=![]() AC,∴PA=PB=PC=PD.
AC,∴PA=PB=PC=PD.
又∵DC=BC,PC=PD,∴△PDC≌△PBC,∴∠DPC=∠BPC.
∵∠APD+∠DPC=180°,∠APD+∠BPC=180°,∴△APD与△BPC互为“顶补等腰三角形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
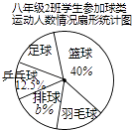
根据图中提供的信息,解答下列问题:
(1)a= , b=;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)小明做作业时,不小心将方程中
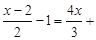 ●的一个常数污染了看不清楚,怎么办呢?
●的一个常数污染了看不清楚,怎么办呢?(1)小红告诉他该方程的解是x=3.那么这个常数应是多少呢?
(2)小芳告诉他该方程的解是负数,并且这个常数是负整数,请你试求该方程的解.(友情提醒:设这个常数为m.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(  ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 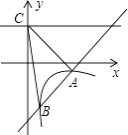
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
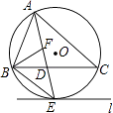
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
相关试题

