【题目】如图,一扇窗户,窗框为铝合金材料,下面是由两个大小相等的长方形窗框构成,上面是由三个大小相等的扇形组成的半圆窗框构成,窗户半圆部分安装彩色玻璃,两个长方形部分安装透明玻璃(本题中π取3,长度单位为米).
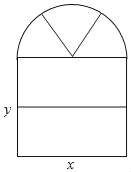
(1)一扇这样窗户一共需要铝合金多少米?(用含x,y的代数式表示)
(2)一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含x,y的代数式表示)
(3)某公司需要购进20扇窗户,在同等质量的前提下,甲、乙两个厂商分别给出如下报价:
铝合金(米/元) | 彩色玻璃(平方米/元) | 透明玻璃(平方米/元) | |
甲厂商 | 200 | 80 | 不超过100平方米的部分,90元/平方米,超过100平方米的部分,70元/平方米 |
乙厂商 | 220 | 60 | 80元/平方米,每购1平方米透明玻璃送0.1米铝合金 |
当x=2,y=3时,该公司在哪家厂商购买窗户合算?
参考答案:
【答案】L=![]() x+2y(2)S=xy+
x+2y(2)S=xy+![]() x2(3)公司在甲厂商购买窗户合算,理由见解析.
x2(3)公司在甲厂商购买窗户合算,理由见解析.
【解析】
(1)求出制作窗框的铝合金材料的总长度即可;
(2)按照矩形与半圆的面积的和即为窗框的面积;
(3)分别求出甲、乙的费用比较大小即可判断.
(1)4x+2y+π![]() x=(
x=(![]() x+2y)米,
x+2y)米,
答:一扇这样窗户一共需要铝合金(![]() x+2y)米;
x+2y)米;
(2)xy+![]() ×π(
×π(![]() )2=(xy+
)2=(xy+![]() x2)米2,
x2)米2,
答:一扇这样窗户一共需要玻璃(xy+![]() x2)平方米;
x2)平方米;
(3)20个这样的窗户共用铝合金为20×(![]() )=340(米),
)=340(米),
共用彩色玻璃为20×![]() =30(平方米),
=30(平方米),
共用透明玻璃为20×2×3=120(平方米),
甲的费用:340×200+100×90+(120-100)×70+30×80=68000+9000+1400+2400=80800元;
乙的费用:(340-120×0.1)×220+120×80+30×60=72160+9600+1800=83560元,
∵80800<83560,
∴公司在甲厂商购买窗户合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
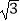 ≈1.7)
≈1.7) 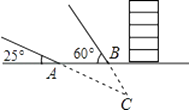
-
科目: 来源: 题型:
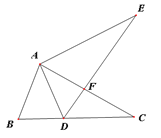
查看答案和解析>>【题目】如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,∠BAD=∠CAE,AC=AE.
(1)求证:△ABC≌△ADE;
(2)若∠B=60°,求证:△ABD是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,∠PFD=∠C,点D到AB和AC的距离相等.求证:点D到PE和PF的距离相等.
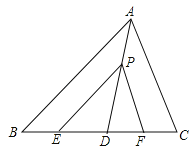
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
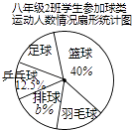
根据图中提供的信息,解答下列问题:
(1)a= , b=;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)小明做作业时,不小心将方程中
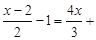 ●的一个常数污染了看不清楚,怎么办呢?
●的一个常数污染了看不清楚,怎么办呢?(1)小红告诉他该方程的解是x=3.那么这个常数应是多少呢?
(2)小芳告诉他该方程的解是负数,并且这个常数是负整数,请你试求该方程的解.(友情提醒:设这个常数为m.)
相关试题

