【题目】如图,双边直尺有两条平行的边,但是没有刻度,可以用来画等距平行线:
![]()
我们也可用工具自制(如图):
![]()
下面是小My同学设计的“过直线外一点作这条直线的平行线”的双边直尺作图过程.
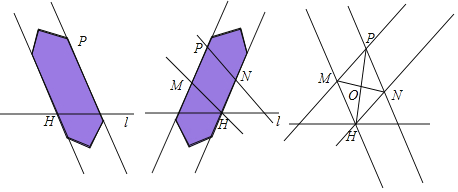
(1)根据小My同学的作图过程,请证明O为PH中点.
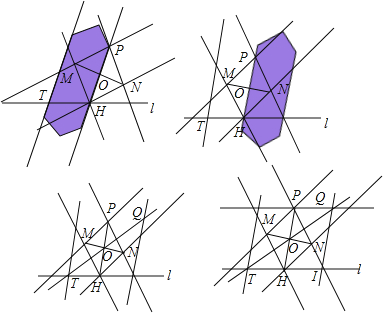
(2)根据小My同学的作图过程,请证明PQ∥l.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据小My同学的作图过程可得,四边形PMHN是平行四边形,根据平行四边形的对角线互相平分,即可得结论;
(2)作OK∥TH交QI于点K,由作图过程可证明△OQK≌△TOH(ASA),可得OQ=OT,进而可以得结论.
解:(1)根据小My同学的作图过程可知:
四边形PMHN是平行四边形,
根据平行四边形的对角线互相平分,
所以O为PH中点.
(2)如图,作OK∥TH交QI于点K,
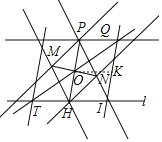
由作图过程可知:
PH∥QI,
∴OK=HI=TH,
∠QOK=∠OTH,
∠OKQ=∠QIH=∠OHT,
∴△OQK≌△TOH(ASA),
∴OQ=OT,
∵OP=OH,
∴四边形PQHT是平行四边形,
∴PQ∥l.
-
科目: 来源: 题型:
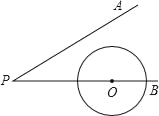
查看答案和解析>>【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
-
科目: 来源: 题型:
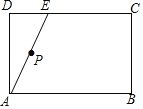
查看答案和解析>>【题目】如图,矩形ABCD中,点E为矩形的边CD上的任意一点,点P为线段AE的中点,连接BP并延长与边AD交于点F,点M为边CD上的一点,且CM=DE,连接FM.
(1)依题意补全图形;
(2)求证∠DMF=∠ABF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是 (用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是 ;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.“穿十条马路连遇十次红灯”是不可能事件
B.任意画一个三角形,其内角和是180°是必然事件
C.某彩票中奖概率为1%,那么买100张彩票一定会中奖
D.“福山福地福人居”这句话中任选一个汉字,这个字是“福”字的概率是
相关试题

