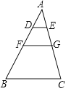
【题目】如图,![]() 中,
中,![]() ,且
,且![]() ,则
,则![]() ________.
________.
参考答案:
【答案】![]()
【解析】
由DE∥FG∥BC,平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,即可判定△ADE∽△AFG∽△ABC,根据相似三角形的面积比等于相似比的平方,即可求得![]() ,
,![]() ,设S△ADE=4x,即可求得S梯形DFGE与S梯形FBCG的值,继而求得S△ADE:S梯形DFGE:S梯形FBCG的值.
,设S△ADE=4x,即可求得S梯形DFGE与S梯形FBCG的值,继而求得S△ADE:S梯形DFGE:S梯形FBCG的值.
∵△ABC中,DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∴![]()
![]() ,
,
∵AD:DF:FB=2:3:4,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设S△ADE=4x,则S△AFG=25x,S△ABC=81x,
∴S梯形DFGE=25x-4x=21x,S梯形FBCG=81x-25x=56x,
∴S△ADE:S梯形DFGE:S梯形FBCG=4:21:56.
故答案为:4:21:56.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是圆圆设计的“作等腰三角形一腰上的高线”的尺规作图过程 .
已知:△
 ,
,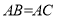 .
.求作:
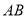 边上的高线.
边上的高线.作法:如图,

①以点
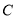 为圆心,
为圆心,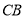 为半径画弧,交
为半径画弧,交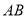 于点
于点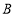 和点
和点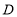 ;
;②分别以点
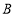 和点
和点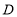 为圆心,大于
为圆心,大于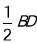 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点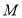 ;
;③作射线
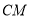 交
交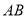 于点
于点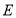 .
.所以线段
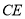 就是所求作的
就是所求作的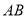 边上的高线.
边上的高线.根据圆圆设计的尺规作图过程,完成下列问题:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵
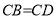 ,
,∴点
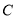 在线段
在线段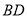 的垂直平分线上(__________) (填推理的依据).
的垂直平分线上(__________) (填推理的依据).∵__________=__________,
∴点
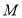 在线段
在线段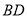 的垂直平分线上.
的垂直平分线上.∴
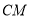 是线段
是线段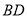 的垂直平分线.
的垂直平分线. ∴
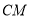 ⊥
⊥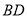 .
.∴线段
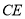 就是
就是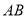 边上的高线.
边上的高线. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有
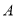 ,
, 两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中
两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中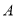 袋中装有2个白球,1个红球;
袋中装有2个白球,1个红球; 袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的
袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的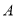 ,
, 两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
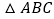 放在每个小正方形的边长为
放在每个小正方形的边长为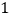 的网格中,点
的网格中,点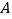 、
、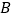 、
、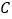 均落在格点上.
均落在格点上.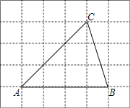
(1)
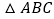 的面积等于________;
的面积等于________;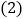 若四边形
若四边形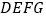 是
是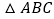 中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明)________.
中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明)________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、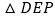 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,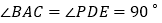 .
.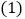 若将
若将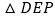 的顶点
的顶点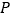 放在
放在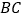 上(如图
上(如图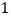 ),
),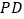 、
、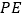 分别与
分别与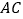 、
、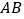 相交于点
相交于点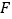 、
、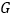 .求证:
.求证: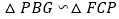 ;
; 若使
若使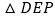 的顶点
的顶点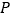 与顶点
与顶点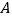 重合(如图
重合(如图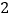 ),
),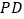 、
、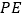 与
与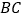 相交于点
相交于点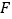 、
、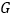 .试问
.试问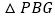 与
与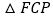 还相似吗?为什么?
还相似吗?为什么?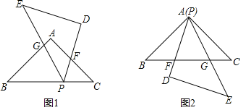
-
科目: 来源: 题型:
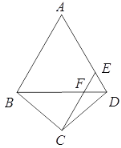
查看答案和解析>>【题目】如图,在四边形
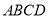 中,
中,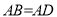 ,
,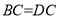 ,
,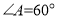 ,点
,点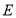 为
为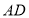 边上一点,连接
边上一点,连接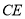 ,
,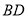 .
. 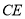 与
与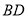 交于点
交于点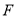 ,且
,且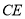 ∥
∥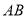 .
.
(1)求证:
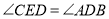 ;
;(2)若
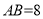 ,
,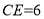 . 求
. 求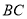 的长 .
的长 .
相关试题

