【题目】为了丰富学生的课外活动,某校决定购买100个篮球和![]() 副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
(1)求每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含![]() 的代数式分别表示出到甲商店和乙商店购买所花的费用;
的代数式分别表示出到甲商店和乙商店购买所花的费用;
(3)请你决策:在哪家商店购买划算?(直接写出结论)
参考答案:
【答案】(1)每个篮球的价格是75元,每副羽毛球拍的价格是50元;(2)甲:50a+7000(元),乙:40a+7500(元);(3)见解析
【解析】
(1)设每个篮球的定价是x元,则每幅羽毛球拍是(x﹣25)元,根据两个篮球与三幅球拍的费用相等列出方程,解方程即可;
(2)根据甲、乙两商店的优惠方案即可求解;
(3)先求出到两家商店购买一样合算时篮球的个数,再根据题意即可求解.
(1)设每个篮球的价格是x元,每幅羽毛球拍的价格是(x-25)元,由题意得:
2x=3(x-25)
解得:x=75.
当x=75时,x-25=50.
答:每个篮球的价格是75元,每副羽毛球拍的价格是50元.
(2)到甲商店购买所花的费用为:75×100+50(![]() )=50a+7000(元);
)=50a+7000(元);
到乙商店购买所花的费用为:75×100+0.8×50×a=40a+7500(元);
(3)令50a+7000=40a+7500,解得:a=50.
当a<50(或10<a<50)时,在甲商店购买划算;
当a=50时,在甲、乙两个商店购买所花的费用一样;
当a>50时,在乙商店购买划算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为()

A.(﹣ ,
,  )
)
B.(﹣ ,
,  )
)
C.(﹣ ,
,  )
)
D.(﹣ ,
,  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DECD,正确的有( )
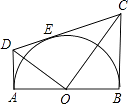
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△BAD中,延长斜边BD到点C,使DC=
 BD,连接AC,若tanB=
BD,连接AC,若tanB=  ,则tan∠CAD的值( )
,则tan∠CAD的值( ) 
A.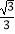
B.
C.
D.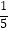
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
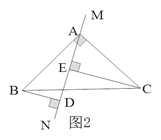
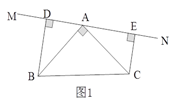
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )
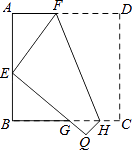
A.4:9
B.2:3
C.3:4
D.9:16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
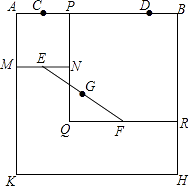
A.1
B.2
C.3
D.6
相关试题

