【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
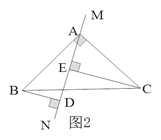
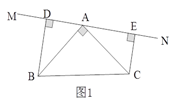
参考答案:
【答案】(1)DE=BD+CE,理由见解析;(2) DE= CE-BD
【解析】试题分析:(1)求出△ABD≌△CEA,根据全等三角形性质得出BD=AE,DA=CE,即可得出答案.
(2)求出△ABD≌△CAE,推出BD=AE,CE=AD,即可求出答案.
试题解析:解:(1)DE=BD+CE.理由如下:
∵BD⊥MN,CE⊥MN,∴∠BDA=∠AEC=90°,∴∠BAD+∠ABD=90°.
又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∴∠ABD=∠CAE .
在△BAD和△ACE中,∵∠BDA=∠AEC=90°,∠ABD=∠CAE,AB=CA,∴△BAD≌△ACE(AAS) ,∴BD=AE,AD=CE.
又∵DE=AE+AD,∴DE=BD+CE.
(2)DE= CE-BD.
同(1)可得△BAD≌△ACE, ∴BD=AE,AD=CE.
又DE= AD –AE,∴DE= CE-BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
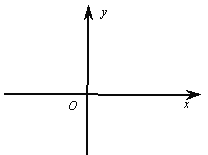
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,-3)到直线y=x+1的直角距离为6,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)求证:BM=AC;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年夏季,湖南省部分地区发生了罕见的旱灾,连续几个月无有效降水.为抗旱救灾,驻湘某部计划为驻地村民新建水渠3600米,为使水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.求实际每天修水渠多少米?(列方程解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:

朝下数字
1
2
3
4
出现的次数
16
20
14
10
【1】计算上述试验中“4朝下”的频率是_________
【2】根据试验结果,投掷一次正四面体,出现2朝下的概率是
 .”的说法正确吗?为什么?
.”的说法正确吗?为什么?【3】随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC=
 ,∠DCE=
,∠DCE= 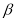 .
.① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究
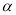 与
与 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时
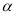 与
与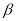 之间的数量关系(不需证明).
之间的数量关系(不需证明).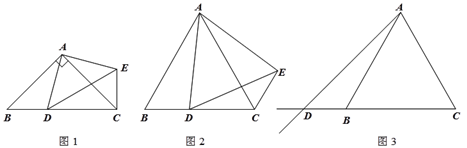
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,点
,点 点
点 分别在射线
分别在射线 ,射线
,射线 上,若点
上,若点 与点
与点 关于
关于 对称,点
对称,点 点
点 关于
关于 对称,
对称,  与
与 相交于点
相交于点 ,有以下命题:①
,有以下命题:① ;②
;② ;③若
;③若 ,
,  ;④
;④ 是等腰直角三角形,则正确的命题有( ).
是等腰直角三角形,则正确的命题有( ).
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个
相关试题

