【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
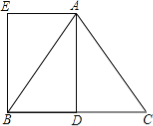
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
参考答案:
【答案】(1)证明见解析;(2)12.
【解析】
试题分析:(1)利用三线合一定理可以证得∠ADB=90°,根据矩形的定义即可证得;
(2)利用勾股定理求得BD的长,然后利用矩形的面积公式即可求解.
试题解析: (1)∵AB=AC,AD是BC的边上的中线,
∴AD⊥BC,
∴∠ADB=90°,
∵四边形ADBE是平行四边形.
∴平行四边形ADBE是矩形;
(2)∵AB=AC=5,BC=6,AD是BC的中线,
∴BD=DC=6×![]() =3,
=3,
在直角△ACD中,
AD=![]() ,
,
∴S矩形ADBE=BDAD=3×4=12.
考点: 1.矩形的判定与性质;2.勾股定理;3.平行四边形的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:

(1)△ODE≌△FCE;
(2)四边形ODFC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
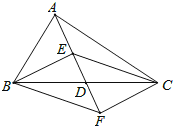
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=4,E为BC的中点,F为AE的中点,过点F作GH⊥AE,分别交AB和CD于G,H,求GF的长,并求
 的值.
的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
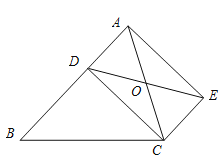
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.
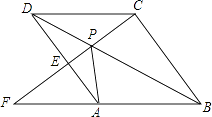
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
相关试题

