【题目】如图,正方形ABCD中,AB=4,E为BC的中点,F为AE的中点,过点F作GH⊥AE,分别交AB和CD于G,H,求GF的长,并求 ![]() 的值.
的值. 
参考答案:
【答案】解:作GM⊥BC垂足为M,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC=4,∠ADC=∠=90°,
在RtABE中,∵DE=DC=2,AD=4
∴AE= ![]() =2
=2 ![]() ,
,
∵AF=EF,
∴AF= ![]() ,
,
∵∠FAG=∠DAE,∠AFG=∠ADE=90°
∴△AFG∽△ADE
得 ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴GF= ![]() ,
,
∵∠GDC=∠D=∠DCM=∠CMD=90°,
∴四边形GMCD是矩形,
∴GM=CD=AD,∠MGD=90°,
∴∠HGM+∠AGF=90°,∠AGF+∠DAE=90°,
∴∠DAE=∠GHM,
在△ADE和△GMH中, ,
,
∴△ADE≌△GMH,
∴HG=AE=2 ![]() ,FH=GH﹣FG=
,FH=GH﹣FG= ![]() ,
,
∴ ![]() =
= ![]() .
.
【解析】先在RT△ADE中求出AE,再利用△AFG∽△ADE得 ![]() =
= ![]() ,即可求出FG,再利用△ADE≌△GMH证明AE=GH即可求出FH即可解决问题.
,即可求出FG,再利用△ADE≌△GMH证明AE=GH即可求出FH即可解决问题.
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:

(1)△ODE≌△FCE;
(2)四边形ODFC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
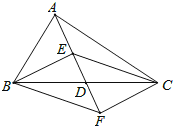
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
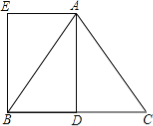
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
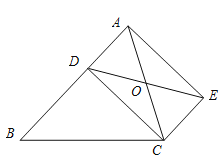
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

相关试题

