【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y1=![]() (x>0)的图象经过菱形对角线的交点A,且交另一边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且交另一边BC交于点F,点A的坐标为(4,2).
(1)求反比例的函数的解析式;
(2)设经过B,C两点的一次函数的解析式为y2=mx+b,求y1<y2的x的取值范围.

参考答案:
【答案】(1)y=![]() ;(2)y1<y2的x的取值范围是x>6.
;(2)y1<y2的x的取值范围是x>6.
【解析】
(1)将点A的坐标代入y=![]() (x>0)中求得k值,即可求得反比例的函数的解析式;(2)先求得点B、点C的坐标,再由待定系数法求得直线BC的解析式,把反比例函数的解析式和直线BC的解析式联立组成方程组,解方程组求得点F的坐标,观察图象即可求解.
(x>0)中求得k值,即可求得反比例的函数的解析式;(2)先求得点B、点C的坐标,再由待定系数法求得直线BC的解析式,把反比例函数的解析式和直线BC的解析式联立组成方程组,解方程组求得点F的坐标,观察图象即可求解.
(1)∵反比例函数y=![]() 的图象经过点A(4,2),
的图象经过点A(4,2),
∴k=2×4=8,
∴反比例函数的解析式为y=![]() ;
;
(2)如图,过点A作AM⊥x轴于点M,过点C作CN⊥x轴于点N,
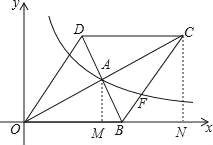
由题意可知,CN=2AM=4,ON=2OM=8,
∴点C的坐标为C(8,4),
设OB=x,则BC=x,BN=8﹣x,
在Rt△CNB中,x2﹣(8﹣x)2=42,
解得:x=5,
∴点B的坐标为B(5,0),
设直线BC的函数表达式为y=ax+b,直线BC过点B(5,0),C(8,4),
∴![]() ,
,
解得: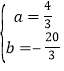 ,
,
∴直线BC的解析式为y=![]() x﹣
x﹣![]() ,
,
根据题意得方程组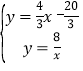 ,
,
解此方程组得:![]() 或
或![]() ,
,
∵点F在第一象限,
∴点F的坐标为F(6,![]() ),
),
∴y1<y2的x的取值范围是x>6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣5,1),B(﹣4,4),C(﹣1,﹣1).
(1)在图1中画出△ABC关于y轴对称的图形△A1B1C1;
(2)直接写出△A1B1C1的面积;
(3)在图2中y轴上找出点P,使PB+PC的值最小(保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,AOBC的顶点A、C的坐标分别为A(﹣2,0)、C(0,3),反比例函数的图象经过点B.
(1)求反比例函数的表达式;
(2)这个反比例函数的图象与一个一次函数的图象交于点B、D(m,1),根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若∠B=∠ACB,CE=5,CF=7,求DB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,点A(1,1),B(3,1),C(3,2),反比例函数y=
 (x>0)的图象经过点D,且与AB相交于点E,
(x>0)的图象经过点D,且与AB相交于点E,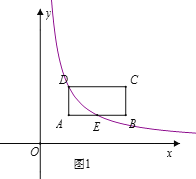
(1)求反比例函数的解析式;
(2)过点C、E作直线,求直线CE的解析式;
(3)如图2,将矩形ABCD沿直线CE平移,使得点C与点E重合,求线段BD扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰
 的三边分别为
的三边分别为 、
、 、
、 ,其中
,其中 ,若关于
,若关于 的方程
的方程 有两个相等的实数根,则
有两个相等的实数根,则 的周长是( )
的周长是( )A. 9 B. 12 C. 9或12 D. 不能确定
-
科目: 来源: 题型:
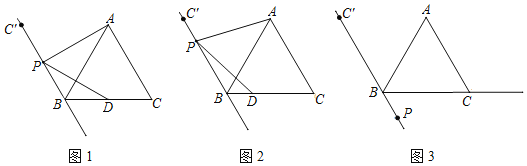
查看答案和解析>>【题目】△ABC是等边三角形,点C关于AB对称的点为C′,点P是直线C′B上的一个动点,连接AP,作∠APD=60°交射线BC于点D.
(1)若点P在线段C′B上(不与点C′,点B重合)
①如图1,当点P是线段C′B的中点时,直接写出线段PD与线段PA的数量关系 .
②如图2,点P是线段C′B上任意一点,证明PD与PA的数量关系.
(2)若点P在线段C′B的延长线上,
①依题意补全图3;
②直接写出线段BD,AB,BP之间的数量关系为: .
相关试题

