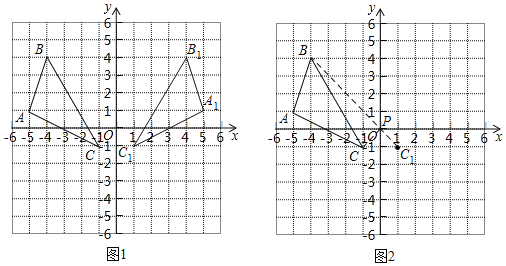
【题目】如图，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别为A（﹣5，1），B（﹣4，4），C（﹣1，﹣1）．

（1）在图1中画出△ABC关于y轴对称的图形△A1B1C1；

（2）直接写出△A1B1C1的面积；

（3）在图2中y轴上找出点P，使PB+PC的值最小（保留作图痕迹）．

参考答案：

【答案】（1）详见解析；（2）7；（3）详见解析．

【解析】

（1）依据轴对称的性质，即可得到△ABC关于y轴对称的图形△A1B1C1；

（2）依据割补法进行计算，即可得到△A1B1C1的面积；

（3）连接C1B，交y轴于点P，连接PC，依据两点之间，线段最短，即可得到PB+PC的值最小．

解：（1）如图1所示，△A1B1C1即为所求；

（2）△A1B1C1的面积为：4×5﹣×2×4﹣×1×3﹣×3×5＝20﹣4﹣1.5﹣7.5＝7；

（3）如图2，连接C1B，交y轴于点P，连接PC，则PB+PC的值最小．

关闭