【题目】如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若∠B=∠ACB,CE=5,CF=7,求DB.

参考答案:
【答案】(1)见解析;(2)3
【解析】
(1)由CF∥AB,可得![]() ,
,![]() ,又由E是边AC的中点,可得△ADE≌△CFE;
,又由E是边AC的中点,可得△ADE≌△CFE;
(2)由(1)CF=AD=7,AE=CE=5,由∠B=∠ACB,可得AB=AC=2CE=10,可得DB的长.
解:
(1)证明:∵E是边AC的中点,
∴AE=CE .
又∵CF∥AB,
∴![]() ,
,![]() .
.
在△ADE与△CFE中,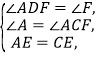
∴△ADE≌△CFE .
(2)解:∵△ADE≌△CFE ,CF=7,
∴CF=AD=7.
又∵∠B=∠ACB,
∴AB=AC.
∵E是边AC的中点,CE=5,
∴AC=2CE=10.
∴AB=10.
∴DB=AB![]() AD=10
AD=10![]() 7=3.
7=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒1cm,设出发的时间为t秒.问t为何值时,△BCP为等腰三角形?

-
科目: 来源: 题型:
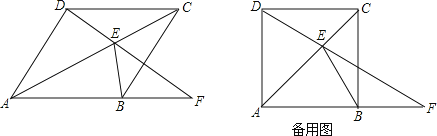
查看答案和解析>>【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%, ①这种商品A的进价为多少元?
②现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次知识竞赛中,甲、乙两人进入了“必答题”环节.规则是:两人轮流答题,每人都要回答20个题,每个题回答正确得a分,回答错误或放弃回答扣b分.当甲、乙两人恰好都答完12个题时,甲答对了8个题,得分为64分;乙答对了9个题,得分为78分.
(1)求a和b的值;
(2)规定此环节得分不低于120分能晋级,甲在剩下的比赛中至少还要答对多少个题才能顺利晋级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:班级
最高分
平均分
中位数
众数
方差
九(1)班
100
94
b
93
12
九(2)班
99
a
95.5
93
8.4
(1)直接写出表中a、b的值:a= , b=;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
相关试题

