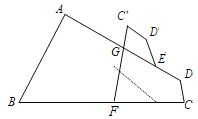
【题目】如图,在四边形 ABCD 中,∠C+∠D=210°,E、F 分别是 AD,BC 上的点,将四边形 CDEF 沿直线 EF 翻折,得到四边形 C′D′EF, C′F 交 AD 于点 G,若△EFG 有两个角相等,则∠EFG=______ °.
参考答案:
【答案】40 或 50
【解析】
作出辅助线,利用翻折前后的角相等得到∠1+∠GFC=∠1+2∠3=150°,再由三角形的内角和定理得到∠3=∠2-30°,分情况讨论即可解题,见详解.
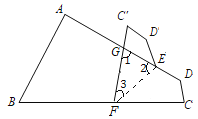
解:连接EF,如下图,由翻折可知,∠3=∠EFC,
∵∠C+∠D=210°,
∴易得∠1+∠GFC=∠1+2∠3=150°,![]()
∵∠1=180°-∠2-∠3,代入![]() 式得∠3=∠2-30°,
式得∠3=∠2-30°,![]()
把![]() 代入
代入![]() 得∠1+2∠2=210°,
得∠1+2∠2=210°,![]()
若∠1=∠2,由![]() 式可得,∠1=∠2=70°,∠3=40°,
式可得,∠1=∠2=70°,∠3=40°,
若∠1=∠3,由![]() 式可得,∠1=∠3=50°,∠2=80°,
式可得,∠1=∠3=50°,∠2=80°,
若∠2=∠3,则![]() 不成立,说明此种情况不存在,
不成立,说明此种情况不存在,
综上∠EFG=40°或50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 朗读者
朗读者 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级 、
、 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩 满分为100分
满分为100分 如图所示.
如图所示.平均数
中位数
众数
九
 班
班85
85
九
 班
班80
 根据图示填写表格;
根据图示填写表格; 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好; 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
-
科目: 来源: 题型:
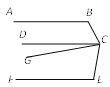
查看答案和解析>>【题目】如图,AB∥CD∥EF,CG平分∠BCE.若∠B=120°,∠GCD=10°,则∠E=___°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
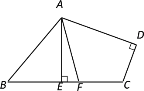
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器
乙型机器
价格(万元/台)
a
b
产量(吨/月)
240
180
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产某种产品,每件产品成本是3元,售价是4元,年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且
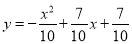 ,如果把利润看作是销售总额减去成本费和广告费,进货都能销售完,试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是是多少万元?
,如果把利润看作是销售总额减去成本费和广告费,进货都能销售完,试写出年利润S(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大,最大年利润是是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表
 单位:环
单位:环 :
:第1次
第2次
第3次
第4次
第5次
第6次
甲
10
9
8
8
10
9
乙
10
10
8
10
7
9
根据表格中的数据,可计算出甲、乙两人的平均成绩都是9环.
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选______名队员参赛.
相关试题

