【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.

(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
参考答案:
【答案】(1)y=-x2+2x+3;y=x+1;(2)能,(0,1)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)利用待定系数法求二次函数解析式、一次函数解析式;
(2)需要分类讨论:①当点E在线段AC上时,点F在点E上方,则F(x,x+3)和②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x-1),然后利用二次函数图象上点的坐标特征可以求得点E的坐标;
(3)过点P作PQ⊥x轴交AC于点Q;过点C作CG⊥x轴于点G,如图1.设Q(x,x+1),则P(x,-x2+2x+3).根据两点间的距离公式可以求得线段PQ=-x2+x+2;最后由图示以及三角形的面积公式知S△APC=-![]() (x-
(x-![]() )2+
)2+![]() ,所以由二次函数的最值的求法可知△APC的面积的最大值.
,所以由二次函数的最值的求法可知△APC的面积的最大值.
试题解析:(1)由抛物线y=-x2+bx+c过点A(-1,0)及C(2,3)得,
![]() ,
,
解得![]() ,
,
故抛物线为y=-x2+2x+3
又设直线为y=kx+n过点A(-1,0)及C(2,3)得
![]() ,
,
解得![]()
故直线AC为y=x+1;
(2)由(1)、(2)得D(1,4),B(1,2),
∵点E在直线AC上,
设E(x,x+1),
①如图2,当点E在线段AC上时,点F在点E上方,
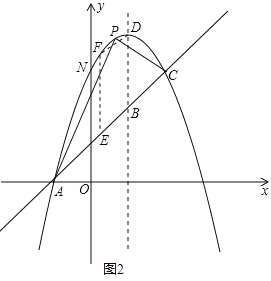
则F(x,x+3),
∵F在抛物线上,
∴x+3=-x2+2x+3,
解得,x=0或x=1(舍去)
∴E(0,1);
②当点E在线段AC(或CA)延长线上时,点F在点E下方,
则F(x,x-1)
由F在抛物线上
∴x-1=-x2+2x+3
解得x=![]() 或x=
或x=![]()
∴E(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
综上,满足条件的点E的坐标为(0,1)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)如图3,过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,设Q(x,x+1),则P(x,-x2+2x+3)
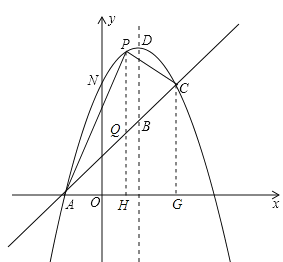
∴PQ=(-x2+2x+3)-(x+1)=-x2+x+2
又∵S△APC=S△APQ+S△CPQ
=![]() PQ
PQ ![]() AG
AG
=![]() (-x2+x+2)×3
(-x2+x+2)×3
=-![]() (x-
(x-![]() )2+
)2+![]()
∴面积的最大值为![]() .
.
-
科目: 来源: 题型:
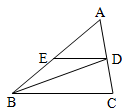
查看答案和解析>>【题目】如图,已知△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠C=80°,求:△BDE各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.
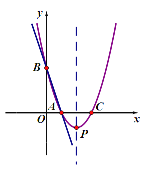
(1)求a,k的值及点C的坐标;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标.
-
科目: 来源: 题型:
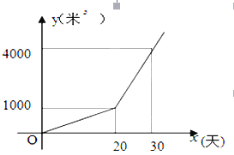
查看答案和解析>>【题目】某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式图
(1)第20天的总用水量为多少米3?
(2)求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A.钝角三角形
B.锐角三角形
C.直角三角形
D.等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数为( )
(1)两点之间,线段最短
(2)多项式ab2﹣3a2+1的次数是5次
(3)若AB=BC,则点B是线段AC的中点
(4)数字0也是单项式.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明.
(1)如图,AB∥CD,CB∥DE.求证:∠B+∠D=180°.

证明:∵AB∥CD,
∴∠B=( ① )( ② );
∵CB∥DE,
∴∠C+∠D=180°( ③ ).
∴∠B+∠D=180°.
(2)如图,∠ABC=∠A′B′C′,BD,B′D′分别是∠ABC,∠A′B′C′的平分线.求证:∠1=∠2.

证明:∵BD, B′D′分别是∠ABC,∠A′B′C′的平分线,
∴∠1=
 ∠ABC,∠2=( ④ )( ⑤ ).
∠ABC,∠2=( ④ )( ⑤ ).又∠ABC=∠A′B′C′,
∴
 ∠ABC=
∠ABC= ∠A′B′C′.
∠A′B′C′.∴∠1=∠2( ⑥ ).
相关试题

