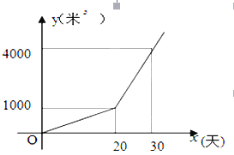
【题目】某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式图
(1)第20天的总用水量为多少米3?
(2)求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
参考答案:
【答案】(1)、1000;(2)、y=50x(0<x<20),y=300x-5000(x≥20);(3)、40.
【解析】
试题分析:(1)、根据题意得出第20天的总用水量;(2)、y与x的函数关系式为分段函数,则需要分两段分别求出函数解析式;(3)、将y=7000代入函数解析式求出x的值.
试题解析:(1)、第20天的总用水量为1000米3
(2)、当0<x<20时,设y=mx ∵函数图象经过点(20,1000),(30,4000) ∴m=50
y与x之间的函数关系式为:y=50x
当x≥20时,设y=kx+b ∵函数图象经过点(20,1000),(30,4000)
∴![]() 解得
解得![]() ∴y与x之间的函数关系式为:y=300x﹣5000
∴y与x之间的函数关系式为:y=300x﹣5000
(3)、当y=7000时, 有7000=300x﹣5000,解得x=40
-
科目: 来源: 题型:
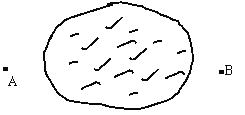
查看答案和解析>>【题目】图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用
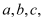 …表示;角度用
…表示;角度用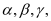 …表示);
…表示);(3)根据你测量的数据,计算A、B两棵树间的距离.
-
科目: 来源: 题型:
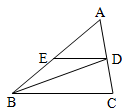
查看答案和解析>>【题目】如图,已知△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠C=80°,求:△BDE各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.
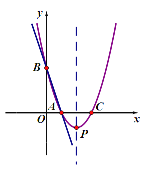
(1)求a,k的值及点C的坐标;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.

(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A.钝角三角形
B.锐角三角形
C.直角三角形
D.等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数为( )
(1)两点之间,线段最短
(2)多项式ab2﹣3a2+1的次数是5次
(3)若AB=BC,则点B是线段AC的中点
(4)数字0也是单项式.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

