搜索
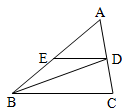
【题目】如图，已知△ABC中，BD是∠ABC的角平分线，DE∥BC，交AB于E，∠A＝60°，∠C=80°，求：△BDE各内角的度数．
参考答案：
【答案】∠ABD=20°；∠BDE=20°；∠BED=140°.
【解析】
试题分析：根据∠A和∠C的度数求出∠ABC的度数，根据BD为角平分线得出∠ABD和∠CBD的度数，根据平行得出∠EDB的度数，最后根据△BDE的内角和求出∠BED的度数.
试题解析：因为∠A＝60°，∠C=80°， 所以∠ABC=180°-∠A-∠C= 40°．
因为BD是∠ABC的角平分线， 所以∠ABD=∠CBD=20°．
又因为DE∥BC， 所以∠BDE=∠CBD=20°． 所以∠BED=180°-∠EBD-∠BDE=140°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（ ）
A.4
B.8
C.10
D.12 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象交于两点A（-2，-5）和B（1，4），且二次函数图象与y轴的交点在直线y=2x+3上，求这两个函数的解析式。
-
科目： 来源： 题型：
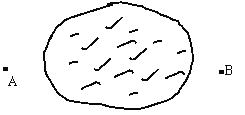
查看答案和解析>>【题目】图为人民公园中的荷花池，现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得)．请你根据所学知识，以卷尺和测角仪为测量工具设计一种测量方案．
要求：(1)画出你设计的测量平面图；
(2)简述测量方法，并写出测量的数据(长度用
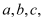…表示；角度用
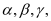…表示)；(3)根据你测量的数据，计算A、B两棵树间的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=-3x+3与x轴、y轴分别交于点A、B，抛物线y=a(x-2)2+k经过点A，B，并与x轴交于另一点C，其顶点为P.
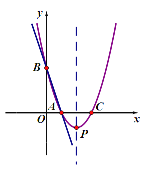
(1)求a,k的值及点C的坐标;
(2)抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标.
-
科目： 来源： 题型：
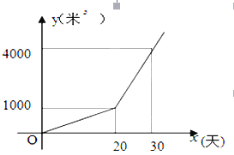
查看答案和解析>>【题目】某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系式图
（1）第20天的总用水量为多少米3？
（2）求y与x之间的函数关系式；
（3）种植时间为多少天时，总用水量达到7000米3？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N，其顶点为D．
（1）抛物线及直线AC的函数关系式；
（2）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；
（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值.
相关试题
