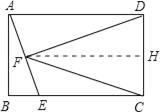
【题目】如图,矩形ABCD中,AB=![]() ,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.

参考答案:
【答案】1、![]() 、2﹣
、2﹣![]()
【解析】
过点C作CM⊥DF,垂足为点M,判断△CDF是等腰三角形,要分类讨论,①CF=CD;②DF=DC;③FD=FC,根据相似三角形的性质进行求解.
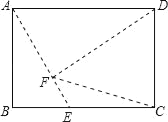
①CF=CD时,过点C作CM⊥DF,垂足为点M,
则CM∥AE,DM=MF,
延长CM交AD于点G,
∴AG=GD=1,
∴CE=1,
∵CG∥AE,AD∥BC,
∴四边形AGCE是平行四边形,
∴CE=AG=1,
∴BE=1
∴当BE=1时,△CDF是等腰三角形;
②DF=DC时,则DC=DF=![]() ,
,
∵DF⊥AE,AD=2,
∴∠DAE=45°,
则BE=![]() ,
,
∴当BE=![]() 时,△CDF是等腰三角形;
时,△CDF是等腰三角形;
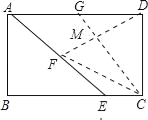
③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB=![]() ,BE=x,
,BE=x,
∴AE=![]() ,
,
AF=![]() ,
,
∵△ADF∽△EAB,
∴![]() ,
,
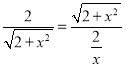 ,
,
x2﹣4x+2=0,
解得:x=2±![]() ,
,
∴当BE=2﹣![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
综上,当BE=1、![]() 、2﹣
、2﹣![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
故答案为:1、![]() 、2﹣
、2﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
-
科目: 来源: 题型:
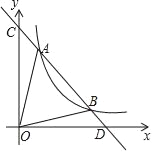
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=
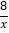 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣
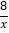 <0的x的取值范围;
<0的x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AB的长是4,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若cos∠DAC=
 ,求弧BC的长.
,求弧BC的长.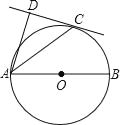
-
科目: 来源: 题型:
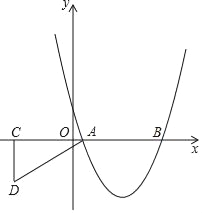
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴分别交于A(1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)过点C(﹣3,0)在x轴下方作x轴的垂线,再以点A为圆心、5为半径长画弧,交先前所作垂线于D,连接AD(如图),将Rt△ACD沿x轴向右平移m个单位,当点D落在抛物线上时,求m的值;
(3)在(2)的条件下,当点D第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法.
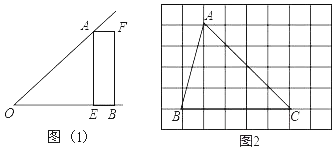
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线.
(2)如图2,在8×6的正方形网格中,请用无刻度直尺画一个与△ABC面积相等,且以BC为边的平行四边形,顶点在格点上.
相关试题

