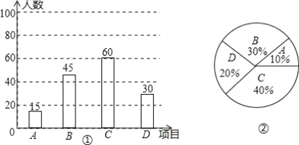
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

参考答案:
【答案】(1)150;(2)45,30%;(3)![]() .
.
【解析】试题分析:(1)用A的人数除以所占的百分比,即可求出调查的学生数;(2)用抽查的总人数减去A、C、D的人数,求出喜欢“立定跳远”的学生人数,再除以被调查的学生数,求出所占的百分比,再画图即可;(3)用A表示男生,B表示女生,画出树形图,再根据概率公式进行计算即可.
试题解析:(1)根据题意,得:15÷10%=150(人),
答:在这项调查中,共调查了150名学生;
(2)本次调查中喜欢“立定跳远”的学生人数为:150﹣15﹣60﹣30=45(人),
“立定跳远”的学生占被调查学生百分比为: ![]() ×100%=30%,
×100%=30%,
补全图形如下:
(3)用A表示男生,B表示女生,画图如下:

共有20种情况,同性别学生的情况是8种,则刚好抽到同性别学生的概率是![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数
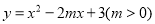 ,有下列说法:
,有下列说法:①如果
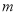 =2,则
=2,则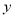 有最小值-1; ②如果当
有最小值-1; ②如果当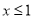 时
时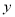 随
随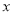 的增大而减小,则
的增大而减小,则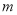 =1;
=1;③如果将它的图象向左平移3个单位后的函数的最小值是-9,则
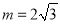 ;
;④如果当
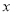 =1时的函数值与
=1时的函数值与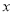 =2015时的函数值相等,则当
=2015时的函数值相等,则当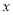 =2016时的函数值为3.其中正确的说法是_____________.(把你认为正确的结论的序号都填上)
=2016时的函数值为3.其中正确的说法是_____________.(把你认为正确的结论的序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点
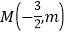 在抛物线上,求
在抛物线上,求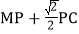 的最小值.
的最小值.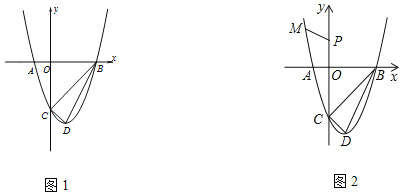
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出
 关于直线x=-1对称的
关于直线x=-1对称的 ,并写出
,并写出 各点坐标.
各点坐标.(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
-
科目: 来源: 题型:
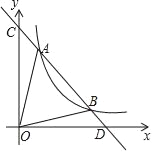
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=
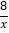 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣
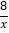 <0的x的取值范围;
<0的x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=
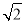 ,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
相关试题

