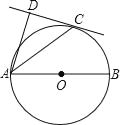
【题目】如图,AB为⊙O的直径,AB的长是4,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若cos∠DAC=![]() ,求弧BC的长.
,求弧BC的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】分析:(1)连接OC,根据切线性质求出OC⊥CD,根据平行线的判定得出AD∥OC,即可求出答案;
(2)求出∠CAB的度数,根据弧长公式求出即可.
详解:(1)证明:连接OC,
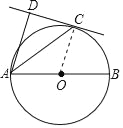
∵DC是⊙O的切线,
∴OC⊥DC,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OAC,
即AC平分∠DAB;
(2)∵∠DAC=∠OAC,cos∠DAC=![]() ,
,
∴∠CAB=30°,
∴∠BOC=60°
∵AB=4,
∴OA=2,
∴弧BC的长为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
-
科目: 来源: 题型:
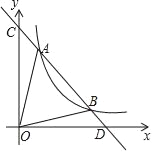
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=
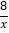 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣
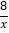 <0的x的取值范围;
<0的x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=
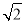 ,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
-
科目: 来源: 题型:
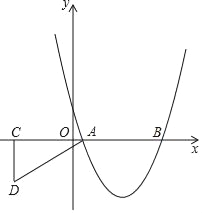
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴分别交于A(1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)过点C(﹣3,0)在x轴下方作x轴的垂线,再以点A为圆心、5为半径长画弧,交先前所作垂线于D,连接AD(如图),将Rt△ACD沿x轴向右平移m个单位,当点D落在抛物线上时,求m的值;
(3)在(2)的条件下,当点D第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法.
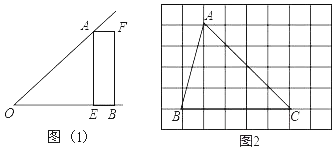
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线.
(2)如图2,在8×6的正方形网格中,请用无刻度直尺画一个与△ABC面积相等,且以BC为边的平行四边形,顶点在格点上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
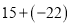 ;
;(2)
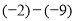 ;
;(3)
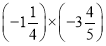
(4)
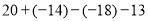 ;
;(5)
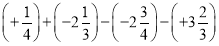
(6)
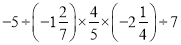 ;
;(7)
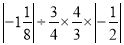
(8)
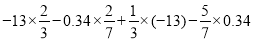
相关试题

