【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价好零售价(单位:元/kg)如下表所示:
品名 | 批发价 | 零售价 |
黄瓜 | 2.4 | 4 |
土豆 | 3 | 5 |
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
参考答案:
【答案】详见解析
【解析】
(1)依题意,根据“购进黄瓜和土豆共40kg”和“用114元”列方程组,求出他当天购进黄瓜和土豆各多少千克.
(2)根据“数量×(零售价-批发价)”可求得卖完这些黄瓜和土豆赚的钱数.
解:(1)设蔬菜经营户从蔬菜批发市场批了黄瓜![]() 千克,土豆
千克,土豆![]() 千克.
千克.
根据题意,得![]() ,解得
,解得![]() .
.
∴他当天购进黄瓜10千克,土豆30千克.
(2)当天卖完这些西红柿和豆角赚的钱数为
10×(4-2.4)+30×(5-3)=76元.
答:他当天卖完这些西红柿和豆角能赚76元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
+5
-2
-4
+13
-10
+16
-9
(1)根据记录的数据可知该厂星期四生产自行车多少辆;
(2)根据记录的数据可知该厂本周实际生产自行车多少辆;
-
科目: 来源: 题型:
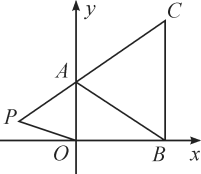
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式
 +(b-3)2=0,(c-4)2≤0.
+(b-3)2=0,(c-4)2≤0.(1)求a,b,c的值;
(2)求出三角形ABC的面积?
(3)如果在第二象限内有一点P(m,
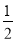 ),那么请用含m的式子表示四边形ABOP的面积;
),那么请用含m的式子表示四边形ABOP的面积;(4)在(3)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(
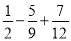 )×(﹣36)
)×(﹣36)(2)计算:100÷(﹣2)2﹣(﹣2)÷(﹣
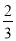 )
)(3)化简:(﹣x2+3xy﹣
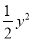 )﹣(﹣
)﹣(﹣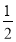 x2+4xy﹣
x2+4xy﹣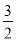 y2)
y2)(4)先化简后求值:x2+(2xy﹣3y2)﹣2(x2+yx﹣2y2),其中x=﹣
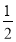 ,y=3.
,y=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+5的图象与反比例函数
 (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数
 (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售甲、乙两种商品,乙种商品每件进价是甲种商品每件进价的
 倍,购进
倍,购进 件甲种商品比购进
件甲种商品比购进 件乙种商品少花
件乙种商品少花 元.
元.(1)求甲、乙两种商品的每件进价分别是多少?
(2)甲、乙两种商品每件售价分别为
 元和
元和 元,超市购进甲、乙两种商品共80件,并且购买甲种商品不多于
元,超市购进甲、乙两种商品共80件,并且购买甲种商品不多于 件,设购进
件,设购进 件甲种商品,获得的总利润为
件甲种商品,获得的总利润为 元,求
元,求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)在(2)的条件下,购买两种商品总进价不超过
 元,问该超市会有多少种进货方案?并求出获利最大的进货方案.
元,问该超市会有多少种进货方案?并求出获利最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在正方形
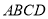 中,点
中,点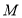 在直线
在直线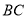 上,连接
上,连接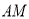 ,作
,作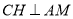 交直线
交直线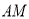 于点
于点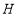 ,点
,点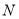 在直线
在直线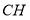 上,连接
上,连接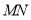 ,且
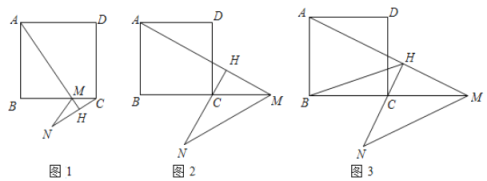
,且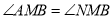 ,
,
(1)如图1,当点
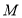 在
在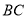 边上,求证:
边上,求证: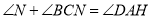 ;
;(2)如图2,当点
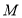 在
在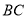 的延长线上,求证:
的延长线上,求证: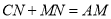 ;
;(3)如图3,在(2)的条件下,连接
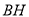 ,若
,若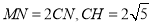 ,求线段
,求线段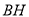 的长.
的长.
相关试题

