【题目】已知:在正方形![]() 中,点
中,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,
,
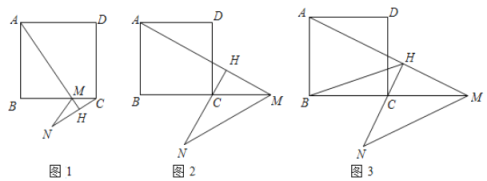
(1)如图1,当点![]() 在
在![]() 边上,求证:
边上,求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上,求证:
的延长线上,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)BH=![]() .
.
【解析】
(1)利用平行线的性质以及三角形的外角的性质证明即可.
(2)如图2中,延长MN,AB交于点K,连接CK,只要证明△AMB≌△KMB(ASA),CN=KN即可解决问题.
(3)如图(3)中,延长MN,AB交于点K,连接CK,CA,BN,AC,延长AC交KM于E,作HF⊥BM于F.想办法证明BC=CM,推出tan∠AMB=tan∠BMK=![]() ,解直角三角形求出HF,BF即可解决问题.
,解直角三角形求出HF,BF即可解决问题.
(1)证明:如图1中,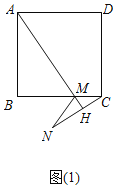
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAH=∠AMB,
∵∠AMB=∠NMB,∠NMB=∠N+∠NCB,
∴∠DAH=∠N+∠NCB.
(2)证明:如图2中,延长MN,AB交于点K,连接CK,CA.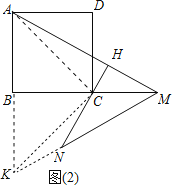
在正方形ABCD中,∠ABC=90°,AD∥BC,
∵∠AMB=∠BMN,
∵∠ABM=∠KBM=90°,BM=BM,
∴△AMB≌△KMB(ASA),
∴BK=AB=BC,∠BKM=∠BAM,AM=KM,
∴∠BKC=∠BCK,
∵CH⊥AM,
∴∠BAM=90°-∠AMB=90°-∠CMH=∠BCN,
∴∠BKM=∠BCN,
∴∠BKC-∠BKM=∠BCK-∠BCN,
∴∠NKC=∠NCK,
∴NK=NC,
∵KM=MN+NK,
∴AM=MN+CN.
(3)解:如图(3)中,延长MN,AB交于点K,连接CK,CA,BN,AC,延长AC交KM于E,作HF⊥BM于F.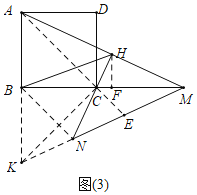
设CN=KN=x,则MN=2x,
∵BK=BC,BN=BN,KN=KC,
∴△BNK≌△BNC(SSS),
∴∠NBK=∠NBC=![]() ∠CBK=45°,
∠CBK=45°,
∵四边形ABC都是正方形,
∴∠BAC=45°,
∴∠NBK=∠BAC,
∴AE∥BN,
∵AB=BK,
∴KN=NE=x,
∴EN=EM=x,
∵CE∥BN,EN=EM,
∴BC=CM,
∴tan∠AMB=tan∠BMK=![]() =
=![]() ,
,
在Rt△CHM中,∵∠CHM=90°,
∴tan∠CMH=![]() ,
,
∵CH=2![]() ,
,
∴MH=4![]() ,
,
∴CM=![]() =10,
=10,
∵![]() CHHM=
CHHM=![]() CMHF,
CMHF,
∴FH=4,FM=8,CF=2,
在Rt△BHF中,BH=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价好零售价(单位:元/kg)如下表所示:
品名
批发价
零售价
黄瓜
2.4
4
土豆
3
5
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+5的图象与反比例函数
 (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数
 (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售甲、乙两种商品,乙种商品每件进价是甲种商品每件进价的
 倍,购进
倍,购进 件甲种商品比购进
件甲种商品比购进 件乙种商品少花
件乙种商品少花 元.
元.(1)求甲、乙两种商品的每件进价分别是多少?
(2)甲、乙两种商品每件售价分别为
 元和
元和 元,超市购进甲、乙两种商品共80件,并且购买甲种商品不多于
元,超市购进甲、乙两种商品共80件,并且购买甲种商品不多于 件,设购进
件,设购进 件甲种商品,获得的总利润为
件甲种商品,获得的总利润为 元,求
元,求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)在(2)的条件下,购买两种商品总进价不超过
 元,问该超市会有多少种进货方案?并求出获利最大的进货方案.
元,问该超市会有多少种进货方案?并求出获利最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
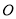 为坐标原点,菱形
为坐标原点,菱形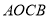 的对角线
的对角线 在
在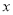 轴上,
轴上,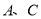 两点分别在第一象限和第四象限.直线
两点分别在第一象限和第四象限.直线 的解析式为
的解析式为 .
.
(1)如图1,求点
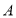 的坐标;
的坐标;(2)如图2,
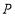 为射线
为射线 上一动点(不与点
上一动点(不与点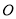 和点
和点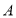 重合),过点
重合),过点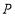 作
作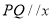 轴交直线
轴交直线 于点
于点 .设线段
.设线段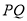 的长度为
的长度为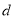 ,点
,点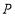 的横坐标为
的横坐标为 ,求
,求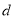 与
与 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量 的取值范围;
的取值范围;(3)如图3,在(2)的条件下,当点
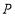 运动到线段
运动到线段 的延长线上时,连接
的延长线上时,连接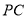 交
交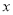 轴于点
轴于点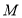 ,连接
,连接 ,
,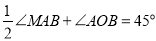 ,延长
,延长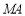 交
交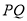 于点
于点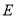 ,过
,过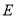 作
作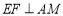 交
交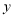 轴于点
轴于点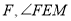 ,的角平分线
,的角平分线 交
交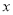 轴于点
轴于点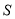 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
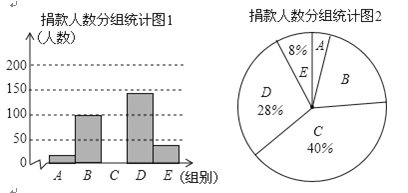
被调查的捐款人数分组统计表:
组别
捐款额x/元
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
______
D
30≤x<40
______
E
40≤x
______
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )
A. 2 B. 3 C. 2或3 D. 不能确定
相关试题

