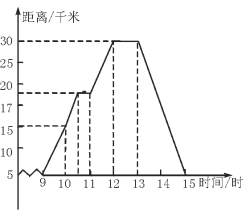
【题目】如图所示,小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)他到达离家最远的地方是什么时间?离家多远?
(3)10时到12时他行驶了多少千米?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
参考答案:
【答案】(1) 图像表示了离家的距离与时间这两个变量之间的关系.其中时间是自变量,离家的距离是因变量; (2) 他到达离家最远的地方是在12时,离家30千米; (3) 10时到12时他行驶了15千米;(4) 他可能在12时到13时间内休息,并吃午餐;(5) 他由离家最远的地方返回时的平均速度是15千米/时
【解析】
(1)根据图象的x轴和y轴即可确定表示了哪两个变量的关系;
(2)首先根据图象找到离家最远的距离,由此即可确定他到达离家最远的地方是什么时间,离家多远;
(3)根据图象首先找到时间为10时和12时离家的距离,然后作差即可;
(4) 如果休息,那么距离没有增加,由此就可以确定在哪段时间内休息,并吃午餐;
(5) 根据返回时所走路程和使用时间即可求出返回时的平均速度.
解:(1) 图像表示了离家的距离与时间这两个变量之间的关系.其中时间是自变量,离家的距离是因变量;
(2)由图象看出他到达离家最远的地方是在12时,离家30千米;
(3)由图象看出10时到12时他行驶了30-15=15千米;
(4)由图象看出12:00~13:00时距离没变且时间较长,得他可能在12时到13时间内休息,并吃午餐;
(5)由图象看出回家时用了2小时,路程是30千米,所以回家的平均速度是30÷2=15(千米/时).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2,
2×3×4×5+1=112=(22+3×2+1)2,
3×4×5×6+1=192=(32+3×3+1)2,
4×5×6×7+1=292=(42+3×4+1)2,
……
(1)根据你的观察,归纳发现规律,写出9×10×11×12+1的结果是________ ;
(2)式子(n-1) n (n+1) (n+2)+1=___________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2(________)
∵AC∥DE(已知)
∴∠1=∠3(________)
故∠2=∠3(________)
∵DF∥AE(已知)
∴∠2=∠5(________)
∴∠3=∠4(________)
∴DE平分∠BDE(________)

-
科目: 来源: 题型:
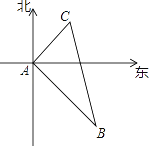
查看答案和解析>>【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
-
科目: 来源: 题型:
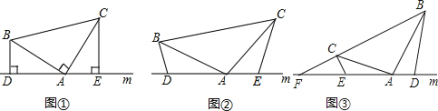
查看答案和解析>>【题目】(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).

(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1;
(3)求点A旋转到点A1所经过的路线长(结果保留π).
相关试题

