【题目】如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1;
(3)求点A旋转到点A1所经过的路线长(结果保留π).
参考答案:
【答案】
(1)解:A(3,4)
(2)解:如图所示:

(3)解:依题意OA= ![]() =5,
=5,
点A到点A1经过的路线长为: ![]()
【解析】(1)先横后纵;(2)按旋转特征画出每个点绕点O顺时针旋转90°后的对应点,顺次连接;(3)点A旋转到点A1所经过的路线长是条弧,利用弧长公式求出.
【考点精析】本题主要考查了弧长计算公式的相关知识点,需要掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.
-
科目: 来源: 题型:
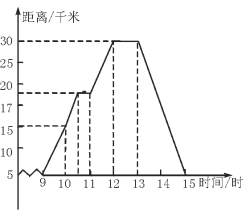
查看答案和解析>>【题目】如图所示,小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)他到达离家最远的地方是什么时间?离家多远?
(3)10时到12时他行驶了多少千米?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
-
科目: 来源: 题型:
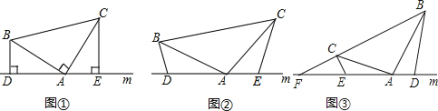
查看答案和解析>>【题目】(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=2x2﹣4x﹣6.
(1)用配方法将y=2x2﹣4x﹣6化成y=a (x﹣h)2+k的形式;并写出对称轴和顶点坐标.
(2)当0<x<4时,求y的取值范围;
(3)求函数图象与两坐标轴交点所围成的三角形的面积. -
科目: 来源: 题型:
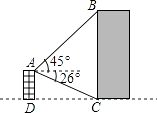
查看答案和解析>>【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
相关试题

