【题目】如图,平行四边形![]() .
.
(1)如图,点![]() 在
在![]() 延长线上,
延长线上,![]() ,求证:点
,求证:点![]() 为
为![]() 中点.
中点.

(2)如图,点![]() 在
在![]() 中点,
中点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() .
.
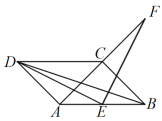
(3)在(2)的条件下,若![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,试判断四边形
,试判断四边形![]() 是否为平行四边形?并证明你的结论(先补全图形再解答).
是否为平行四边形?并证明你的结论(先补全图形再解答).

参考答案:
【答案】(1)见详解;(2)见详解;(3)四边形ACPE是平行四边形,补图与证明见详解.
【解析】
(1)先由平行四边形ABCD可得AD∥BC,AD=BC,再证四边形BDEC为平行四边形可得BC=DE,再等量代换即可得证;
(2)连接CE,根据三线合一可证得∠AEC=90°,结合∠DEF=90°,可得∠AED=∠CEF,根据∠ACB=90°,E为AB中点可得CE=AE,再结合∠DAE=∠ECF=135°即可证得△DAE≌△ECF进而得证;
(3)四边形ACPE是平行四边形,理由如下:先证得∠CEB=∠EBP=∠ECP=90°可得矩形BECP,进而得CP=BE等量代换得AE=CP,再结合AE∥CP即可得证.
证明:(1)∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵AD∥BC,CE∥BD,
∴四边形BDEC为平行四边形,
∴BC=DE,
又∵AD=BC,
∴AD= DE,
∴点D为AE中点.
(2)如图,连接CE,
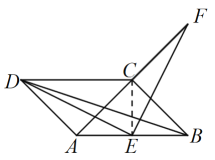
∵AD⊥AC,AD∥BC,
∴∠ACB=∠DAC=90°,
∵AD=BC,AD=AC,
∴BC=AC,
∵BC=AC,点E为AB中点,
∴CE⊥AB,
∴∠AEC=∠BEC=90°,
∴∠AED+∠DEC=90°,
∵ED⊥EF,
∴∠CEF+∠DEC=∠DEF=90°,
∴∠CEF=∠AED,
∵∠ACB=90°,BC=AC,
∴∠CAB=∠CBA=45°,
∴∠DAE=∠DAC+∠CAB=135°,
∵∠ACB=90°,点E为AB中点,
∴CE=AE=![]() AB,
AB,
∴∠ACE=∠CAB=45°,
∴∠FCE=180°-∠ACE=135°,
∴∠FCE=∠DAE,
在△DAE和△FCE中,
 ,
,
∴△DAE≌△FCE(ASA),
∴DE=EF.
(3)如图,

四边形ACPE是平行四边形,理由如下:
∵△DAE≌△FCE,
∴AD=CF,
∵AD=BC,
∴BC=CF,
又∵∠FCB=180°-∠ACB=90°,
∴∠CBF=∠CFB=45°,
∵∠CBA=45°,
∴∠EBF=∠CBF+∠CBA=90°,
∵AB∥CD,∠BEC=90°,
∴∠ECP=180°-∠BEC=90°,
∴∠ECP=∠BEC=∠EBF=90°,
∴四边形BECP为矩形,
∴BE=CP,
又∵AE=BE,
∴AE=CP,
∵AE=CP,AE∥CP,
∴四边形ACPE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的发展,智能制造逐渐成为一种可能的生产方式.重庆某电子零部件生产商原来采用自动化程度较低的传统生产方式,工厂有熟练工人和新工人共100人,熟练工平均每天能生产30个零件,新工人平均每天能生产20个零件,所有工人刚好用30天完成了一项7.2万个零件的生产任务.
(1)请问该工厂有熟练工,新工人各多少人?(请列二元一次方程组解题)
(2)今年,某自动化技术团队为工厂提供了A、B两种不同型号的机器人,且两种机器人都可以单独完成零件的生产.已知A型机器人的售价为80万元/台,B型机器人的售价为120万元/台.工厂准备采购价值840万元的机器人设备,两种机器人都至少购买一台,若840万元刚好用完,求出所有可能的购买方案.
(3)已知一个零件的毛利润(只扣除了原材料成本)为10元,若选择传统生产方式,熟练工每月基本工资3000元,新工人每月基本工资2000元,在基本工资之上,工厂还需额外支付计件工资5元/件,传统生产方式的设备成本忽略不计.若选择智能制造方式生产,A型机器人每月生产零件1.5万个,B型机器人每月能生产零件2.7万个,1台A型机器人需要8名技术人员操控,一台B型机器人需要12名技术人员操控,技术人员每人工资1万元,实际生产过程中,一台A型机器人平均每月的总成本为6万元(包含所有设备成本和维护成本),一台B型机器人平均每月的总成本为8万元(包含所有设备成本和维护成本).请你比较传统的生产方式和(2)中的所有购买方案对应的智能生产方式,哪种生产方式每月的总利润最大,最大利润为多少万元?(注:每月均按30天计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=
 ,求
,求 的值.
的值.(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

-
科目: 来源: 题型:
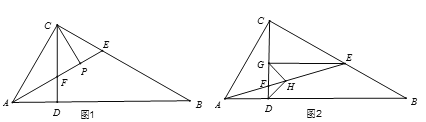
查看答案和解析>>【题目】已知:在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E是BC上一点,连接AE交CD于点F.
(1)如图1,若AE平分∠CAB,CP平分∠BCD,求证:FP=EP;
(2)如图2,若CE=CA,过点E作EG⊥CD于点G,点H为AE的中点,连接DH,GH,判断△GDH的形状,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )
①△CDF≌△EBC;
②△CEF是等边三角形;
③∠CDF=∠EAF;
④CE∥DF

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:

 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的. 若点
若点 是点
是点 通过
通过 中的平移变换得到的,求
中的平移变换得到的,求 的值.
的值.
相关试题

