【题目】如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )
①△CDF≌△EBC;
②△CEF是等边三角形;
③∠CDF=∠EAF;
④CE∥DF

A.1B.2C.3D.4
参考答案:
【答案】C
【解析】
利用“边角边”证明△CDF和△EBC全等,判定①正确;同理求出△CDF和△EAF全等,根据全等三角形对应边相等可得![]() ,判定△ECF是等边三角形,判定②正确;利用“8字型”判定③正确;若
,判定△ECF是等边三角形,判定②正确;利用“8字型”判定③正确;若![]() ,则C、F、A三点共线,故④错误;即可得出答案.
,则C、F、A三点共线,故④错误;即可得出答案.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∵![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,故①正确;
,故①正确;
在![]() 中,设AE交CD于O,AE交DF于K,如图:
中,设AE交CD于O,AE交DF于K,如图:

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
故③正确;
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,故②正确;
是等边三角形,故②正确;
则![]() ,
,
若![]() 时,
时,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
则C、F、A三点共线
已知中没有给出C、F、A三点共线,故④错误;
综上所述,正确的结论有①②③.
故选:C.
-
科目: 来源: 题型:
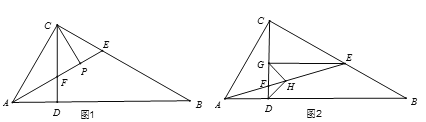
查看答案和解析>>【题目】已知:在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E是BC上一点,连接AE交CD于点F.
(1)如图1,若AE平分∠CAB,CP平分∠BCD,求证:FP=EP;
(2)如图2,若CE=CA,过点E作EG⊥CD于点G,点H为AE的中点,连接DH,GH,判断△GDH的形状,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 .
.(1)如图,点
 在
在 延长线上,
延长线上, ,求证:点
,求证:点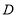 为
为 中点.
中点.
(2)如图,点
 在
在 中点,
中点, 是
是 延长线上一点,且
延长线上一点,且 ,求证:
,求证: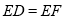 .
.
(3)在(2)的条件下,若
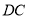 的延长线与
的延长线与 交于点
交于点 ,试判断四边形
,试判断四边形 是否为平行四边形?并证明你的结论(先补全图形再解答).
是否为平行四边形?并证明你的结论(先补全图形再解答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:

 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的. 若点
若点 是点
是点 通过
通过 中的平移变换得到的,求
中的平移变换得到的,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图17-Z-11,小红同学要测量A,C两地的距离,但A,C之间有一水池,不能直接测量,于是她在A,C同一水平面上选取了一点B,点B可直接到达A,C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A,C两地之间的距离.(结果精确到1米,参考数据:
 ≈4.6)
≈4.6)
图17-Z-11
-
科目: 来源: 题型:
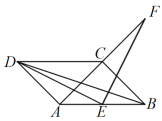
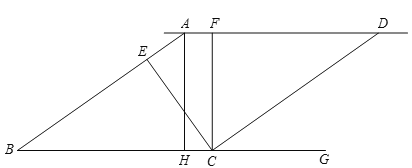
查看答案和解析>>【题目】如图,已知
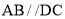 ,
,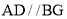 ,
,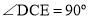 ,点E在线段AB上,
,点E在线段AB上,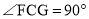 ,点F在直线AD上,
,点F在直线AD上,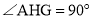 .
.
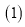 若
若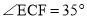 ,求
,求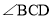 的度数;
的度数;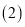 找出图中与
找出图中与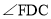 相等的角,并说明理由;
相等的角,并说明理由;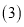 在
在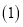 的条件下,点
的条件下,点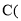 不与点B、H重合
不与点B、H重合 从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出
从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出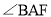 的度数
的度数 不必说明理由
不必说明理由 .
.
相关试题

