【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得![]() = tanD=
= tanD=![]() ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得![]() ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
试题解析:(1)证明:作OF⊥AB于F
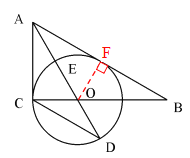
∵AO是∠BAC的角平分线,∠ACB=90
∴OC=OF
∴AB是⊙O的切线
(2)连接CE
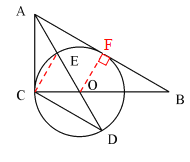
∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴![]() = tanD=
= tanD=![]()
(3)先在△ACO中,设AE=x,
由勾股定理得
(x+3)="(2x)" +3 ,解得x="2,"
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得![]() ,
,
设BO=y BF=z
![]()
即4z=9+3y,4y=12+3z
解得z=![]() y=
y=![]()
∴AB=![]() +4=
+4=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数是二次函数的是( )
A. y=2x+2 B. y=﹣2x C. y=x2+2 D. y=x﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形的相似比是2:3,较小三角形的面积为4cm2,那么较大三角形的面积为_____cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a<0时,不等式ax<|a|的解集为( )
A. x>1 B. x<1 C. x>-1 D. x<-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
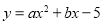 (
(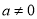 )经过点
)经过点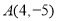 ,与
,与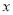 轴的负半轴交于点
轴的负半轴交于点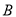 ,与
,与 轴交于点
轴交于点 ,且
,且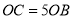 ,抛物线的顶点为
,抛物线的顶点为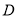 .
.
(1)求这条抛物线的表达式;
(2)联结
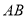 、
、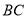 、
、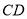 、
、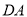 ,求四边形
,求四边形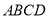 的面积;
的面积;(3)如果点
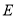 在
在 轴的正半轴上,且
轴的正半轴上,且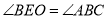 ,求点
,求点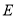 的坐标.
的坐标. -
科目: 来源: 题型:
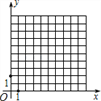
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作:
在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
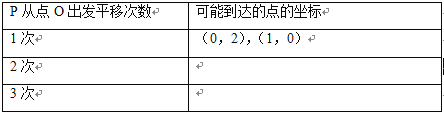
(2)观察发现:
设点P(x,y),任一次平移,点P可能到达的点的纵、横坐标都满足一定的关系式.
例如:平移1次后2x+y= _________;平移2次后2x+y= ;平移3次后2x+y= ;……由此我们知道,平移n次后点P的坐标都满足一定的关系式是 ;
(3)探索运用:
点P从点O出发经过n次平移后到达点Q,若点Q的纵坐标比横坐标大6,并且P平移的路径长不小于50,不超过56,请直接写出Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当k____时,不等式(k+2)x|k|-1+5<0是一元一次不等式.
相关试题

